Function for prediction at new locations for single-species hierarchical distance sampling models
predict.DS.RdThe function predict collects posterior predictive samples for a set of new locations given an object of class `DS`. Prediction is possible for both the latent abundance state as well as detection.
Usage
# S3 method for DS
predict(object, X.0, ignore.RE = FALSE, type = 'abundance', ...)Arguments
- object
an object of class DS
- X.0
the design matrix of covariates at the prediction locations. This should include a column of 1s for the intercept if an intercept is included in the model. If random effects are included in the abundance (or detection if
type = 'detection') portion of the model, the levels of the random effects at the new locations should be included as a column in the design matrix. The ordering of the levels should match the ordering used to fit the data inDS. Columns should correspond to the order of how covariates were specified in the corresponding formula argument ofDS. Column names of all variables must match the names of variables used when fitting the model (for the intercept, use'(Intercept)').- ignore.RE
logical value that specifies whether or not to remove random abundance (or detection if
type = 'detection') effects from the subsequent predictions. IfTRUE, random effects will be included. IfFALSE, random effects will be set to 0 and predictions will only be generated from the fixed effects.- type
a quoted keyword indicating what type of prediction to produce. Valid keywords are 'abundance' to predict latent abundance and expected abundance values (this is the default), or 'detection' to predict detection probability given new values of detection covariates.
- ...
currently no additional arguments
Note
When ignore.RE = FALSE, both sampled levels and non-sampled levels of random effects are supported for prediction. For sampled levels, the posterior distribution for the random intercept corresponding to that level of the random effect will be used in the prediction. For non-sampled levels, random values are drawn from a normal distribution using the posterior samples of the random effect variance, which results in fully propagated uncertainty in predictions with models that incorporate random effects.
Author
Jeffrey W. Doser doserjef@msu.edu,
Value
A list object of class predict.DS. When type = 'abundance', the list consists of:
- mu.0.samples
a
codaobject of posterior predictive samples for the expected abundance values, or expected abundance per unit area (i.e., density) values when an offset was used when fitting the model withDS().- N.0.samples
a
codaobject of posterior predictive samples for the latent abundance values. These will be in the same units asmu.0.samples.
When type = 'detection', the list consists of:
- sigma.0.samples
a
codaobject of posterior predictive samples for sigma (the parameter controlling detection probability).
The return object will include additional objects used for standard extractor functions.
Examples
set.seed(123)
J.x <- 10
J.y <- 10
J <- J.x * J.y
# Number of distance bins from which to simulate data.
n.bins <- 5
# Length of each bin. This should be of length n.bins
bin.width <- c(.10, .10, .20, .3, .1)
# Abundance coefficients
beta <- c(1.0, 0.2, 0.3, -0.2)
p.abund <- length(beta)
# Detection coefficients
alpha <- c(-1.0, -0.3)
p.det <- length(alpha)
# Detection decay function
det.func <- 'halfnormal'
mu.RE <- list()
p.RE <- list()
sp <- FALSE
family <- 'NB'
kappa <- 0.1
offset <- 1.8
transect <- 'point'
dat <- simDS(J.x = J.x, J.y = J.y, n.bins = n.bins, bin.width = bin.width,
beta = beta, alpha = alpha, det.func = det.func, kappa = kappa,
mu.RE = mu.RE, p.RE = p.RE, sp = sp, family = family,
offset = offset, transect = transect)
# Split into fitting and prediction data set
pred.indx <- sample(1:J, round(J * .25), replace = FALSE)
y <- dat$y[-pred.indx, ]
# Abundance covariates
X <- dat$X[-pred.indx, ]
# Prediction covariates
X.0 <- dat$X[pred.indx, ]
# Detection covariates
X.p <- dat$X.p[-pred.indx, ]
dist.breaks <- dat$dist.breaks
covs <- cbind(X, X.p)
colnames(covs) <- c('int.abund', 'abund.cov.1', 'abund.cov.2', 'abund.cov.3',
'int.det', 'det.cov.1')
data.list <- list(y = y,
covs = covs,
dist.breaks = dist.breaks,
offset = offset)
# Priors
prior.list <- list(beta.normal = list(mean = 0, var = 10),
alpha.normal = list(mean = 0,
var = 10),
kappa.unif = c(0, 100))
# Starting values
inits.list <- list(alpha = 0,
beta = 0,
kappa = 1)
# Tuning values
tuning <- list(beta = 0.1, alpha = 0.1, beta.star = 0.3, alpha.star = 0.1,
kappa = 0.2)
out <- DS(abund.formula = ~ abund.cov.1 + abund.cov.2 + abund.cov.3,
det.formula = ~ det.cov.1,
data = data.list,
n.batch = 10,
batch.length = 25,
inits = inits.list,
family = 'NB',
det.func = 'halfnormal',
transect = 'point',
tuning = tuning,
priors = prior.list,
accept.rate = 0.43,
n.omp.threads = 1,
verbose = TRUE,
n.report = 100,
n.burn = 100,
n.thin = 1,
n.chains = 1)
#> ----------------------------------------
#> Preparing to run the model
#> ----------------------------------------
#> N is not specified in initial values.
#> Setting initial values based on observed data
#> ----------------------------------------
#> Model description
#> ----------------------------------------
#> Negative Binomial HDS model with 75 sites.
#>
#> Samples per Chain: 250 (10 batches of length 25)
#> Burn-in: 100
#> Thinning Rate: 1
#> Number of Chains: 1
#> Total Posterior Samples: 150
#>
#> Source compiled with OpenMP support and model fit using 1 thread(s).
#>
#> Adaptive Metropolis with target acceptance rate: 43.0
#> ----------------------------------------
#> Chain 1
#> ----------------------------------------
#> Sampling ...
#> Batch: 10 of 10, 100.00%
summary(out)
#>
#> Call:
#> DS(abund.formula = ~abund.cov.1 + abund.cov.2 + abund.cov.3,
#> det.formula = ~det.cov.1, data = data.list, inits = inits.list,
#> priors = prior.list, tuning = tuning, n.batch = 10, batch.length = 25,
#> accept.rate = 0.43, family = "NB", transect = "point", det.func = "halfnormal",
#> n.omp.threads = 1, verbose = TRUE, n.report = 100, n.burn = 100,
#> n.thin = 1, n.chains = 1)
#>
#> Samples per Chain: 250
#> Burn-in: 100
#> Thinning Rate: 1
#> Number of Chains: 1
#> Total Posterior Samples: 150
#> Run Time (min): 0.0027
#>
#> Abundance (log scale):
#> Mean SD 2.5% 50% 97.5% Rhat ESS
#> (Intercept) 0.1046 0.2879 -0.4253 0.1116 0.6157 NA 4
#> abund.cov.1 -0.1573 0.3773 -0.7976 -0.0570 0.4275 NA 3
#> abund.cov.2 0.0367 0.1874 -0.3072 0.0096 0.3936 NA 13
#> abund.cov.3 -0.1717 0.4106 -0.8580 -0.1479 0.4608 NA 3
#>
#> Detection (log scale):
#> Mean SD 2.5% 50% 97.5% Rhat ESS
#> (Intercept) -0.5565 0.1988 -0.8976 -0.5943 -0.1545 NA 5
#> det.cov.1 -0.3956 0.1539 -0.7339 -0.3412 -0.1907 NA 3
#>
#> NB overdispersion:
#> Mean SD 2.5% 50% 97.5% Rhat ESS
#> kappa 0.1262 0.0295 0.0781 0.1163 0.1837 NA 20
# Predict at new locations ------------------------------------------------
colnames(X.0) <- c('intercept', 'abund.cov.1', 'abund.cov.2', 'abund.cov.3')
out.pred <- predict(out, X.0)
mu.0.quants <- apply(out.pred$mu.0.samples, 2, quantile, c(0.025, 0.5, 0.975))
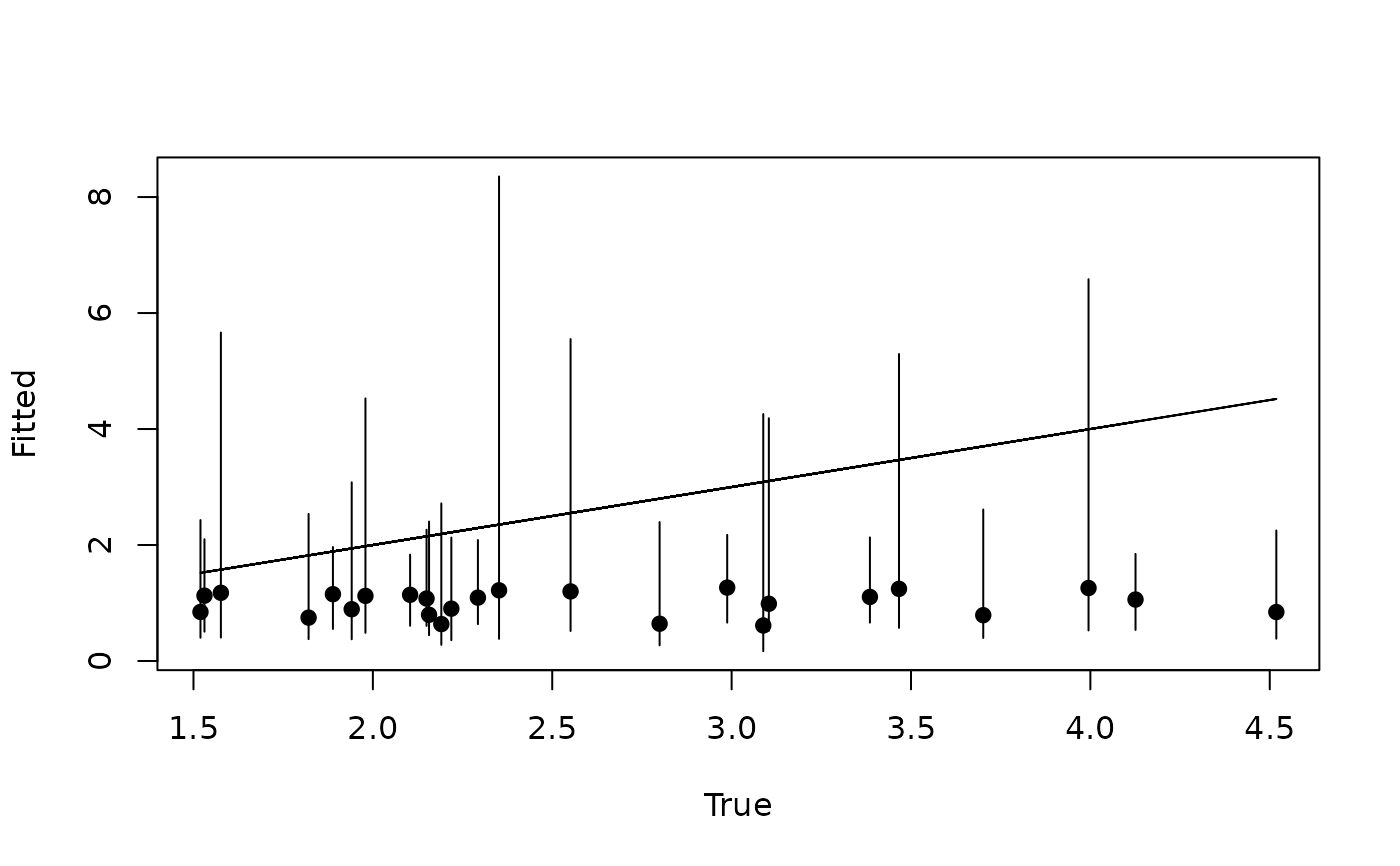
plot(dat$mu[pred.indx], mu.0.quants[2, ], pch = 19, xlab = 'True',
ylab = 'Fitted', ylim = c(min(mu.0.quants), max(mu.0.quants)))
segments(dat$mu[pred.indx], mu.0.quants[1, ], dat$mu[pred.indx], mu.0.quants[3, ])
lines(dat$mu[pred.indx], dat$mu[pred.indx])