Function for prediction at new locations for univariate spatial GLMMs

The function predict collects posterior predictive samples for a set of new locations given an object of class `spAbund`.

Usage

# S3 method for spAbund
predict(object, X.0, coords.0, n.omp.threads = 1, 
        verbose = TRUE, n.report = 100, 
        ignore.RE = FALSE, z.0.samples, include.sp = TRUE, ...)

Arguments

object: an object of class spAbund
X.0: the design matrix of covariates at the prediction locations. This should be a three-dimensional array, with dimensions corresponding to site, replicate, and covariate, respectively. Note that the first covariate should consist of all 1s for the intercept if an intercept is included in the model. If random effects are included in the spAbundance portion of the model, the levels of the random effects at the new locations/time periods should be included as an element of the three-dimensional array. The ordering of the levels should match the ordering used to fit the data in spAbund. The covariates should be organized in the same order as they were specified in the corresponding formula argument of spAbund. Names of the third dimension (covariates) of any random effects in X.0 must match the name of the random effects used to fit the model, if specified in the corresponding formula argument of spAbund. See example below. If there is only one replicate per location, the design matrix can be a two-dimensional matrix instead of a three-dimensional array.
coords.0: the spatial coordinates corresponding to X.0. Note that spAbundance assumes coordinates are specified in a projected coordinate system.
n.omp.threads: a positive integer indicating the number of threads to use for SMP parallel processing. The package must be compiled for OpenMP support. For most Intel-based machines, we recommend setting n.omp.threads up to the number of hyperthreaded cores. Note, n.omp.threads > 1 might not work on some systems.
verbose: if TRUE, model specification and progress of the sampler is printed to the screen. Otherwise, nothing is printed to the screen.
n.report: the interval to report sampling progress.
ignore.RE: logical value that specifies whether or not to remove unstructured random effects from the subsequent predictions. If TRUE, unstructured random effects will be included. If FALSE, unstructured random effects will be set to 0 and predictions will only be generated from the fixed effects.
z.0.samples: a matrix with rows corresponding to MCMC samples and columns corresponding to prediction locations containing the full posterior samples of the predicted binary portion of a zero-inflated Gaussian model. In the context of abundance models, this typically corresponds to estimates of the presence or absence of the species at the location. When using spOccupancy to generate the first stage samples of the zero-inflated Gaussian model, this is the object contained in the z.0.samples object of the predition function for the spOccupancy object. Ignored for all model types other than zero-inflated Gaussian.
include.sp: a logical value used to indicate whether spatial random effects should be included in the predictions. By default, this is set to TRUE. If set to FALSE, predictions are given using the covariates and any unstructured random effects in the model. If FALSE, the coords.0 argument is not required.
...: currently no additional arguments

Note

When ignore.RE = FALSE, both sampled levels and non-sampled levels of random effects are supported for prediction. For sampled levels, the posterior distribution for the random effect corresponding to that level of the random effect will be used in the prediction. For non-sampled levels, random values are drawn from a normal distribution using the posterior samples of the random effect variance, which results in fully propagated uncertainty in predictions with models that incorporate random effects.

Author

Jeffrey W. Doser doserjef@msu.edu,
Andrew O. Finley finleya@msu.edu,

Value

A list object of class predict.spAbund. The list consists of:

mu.0.samples: a three-dimensional object of posterior predictive samples for the expected spAbundance values with dimensions corresponding to posterior predictive sample, site, and replicate. Note if an offset was used when fitting the model with spAbund, the abundance values are reported per unit of the offset.
y.0.samples: a three-dimensional object of posterior predictive samples for the spAbundance values with dimensions corresponding to posterior predictive sample, site, and replicate. These will be in the same units as mu.0.samples.
w.0.samples: a coda object of posterior predictive samples for the latent spatial random effects.

The return object will include additional objects used for standard extractor functions.

Examples

set.seed(1010)
J.x <- 15
J.y <- 15
J <- J.x * J.y
n.rep <- sample(1, J, replace = TRUE)
beta <- c(0, -1.5, 0.3, -0.8)
p.spAbund <- length(beta)
mu.RE <- list()
kappa <- 0.5
sp <- TRUE 
sigma.sq <- 0.5
phi <- 3 / .5
family <- 'NB'
cov.model = 'exponential'
dat <- simAbund(J.x = J.x, J.y = J.y, n.rep = n.rep, beta = beta, 
                kappa = kappa, mu.RE = mu.RE, sp = sp, family = 'NB', 
                sigma.sq = sigma.sq, phi = phi, cov.model = cov.model)

# Split into fitting and prediction data set
pred.indx <- sample(1:J, round(J * .25), replace = FALSE)
y <- dat$y[-pred.indx, ]
# Abundance covariates
X <- dat$X[-pred.indx, , , drop = FALSE]
# Prediction covariates
X.0 <- dat$X[pred.indx, , ]
coords <- as.matrix(dat$coords[-pred.indx, ])
coords.0 <- as.matrix(dat$coords[pred.indx, ])

abund.covs <- list(int = X[, , 1], 
                   abund.cov.1 = X[, , 2], 
                   abund.cov.2 = X[, , 3], 
                   abund.cov.3 = X[, , 4])

data.list <- list(y = y, covs = abund.covs, coords = coords)

# Priors
prior.list <- list(beta.normal = list(mean = 0, var = 100),
                   kappa.unif = c(0.001, 10)) 
# Starting values
inits.list <- list(beta = 0, kappa = kappa)

n.batch <- 5
batch.length <- 25
n.burn <- 0
n.thin <- 1
n.chains <- 1

out <- spAbund(formula = ~ abund.cov.1 + abund.cov.2 + abund.cov.3,
               data = data.list, 
               n.batch = n.batch, 
               batch.length = batch.length, 
               inits = inits.list, 
               priors = prior.list, 
               accept.rate = 0.43, 
               n.neighbors = 5,
               cov.model = cov.model,
               n.omp.threads = 1, 
               verbose = TRUE, 
               n.report = 1,
               n.burn = n.burn,
               n.thin = n.thin,
               n.chains = n.chains) 
#> ----------------------------------------
#> 	Preparing to run the model
#> ----------------------------------------
#> No prior specified for phi.unif.
#> Setting uniform bounds based on the range of observed spatial coordinates.
#> No prior specified for sigma.sq.
#> Using an inverse-Gamma prior with the shape parameter set to 2 and scale parameter to 1.
#> phi is not specified in initial values.
#> Setting initial value to random value from the prior distribution
#> sigma.sq is not specified in initial values.
#> Setting initial value to random value between 0.05 and 3 or the user-specified bounds if using a uniform prior.
#> w is not specified in initial values.
#> Setting initial value to 0
#> ----------------------------------------
#> 	Building the neighbor list
#> ----------------------------------------
#> ----------------------------------------
#> Building the neighbors of neighbors list
#> ----------------------------------------
#> ----------------------------------------
#> 	Model description
#> ----------------------------------------
#> Spatial NNGP Poisson Abundance model fit with 169 sites.
#> 
#> Samples per Chain: 125 (5 batches of length 25)
#> Burn-in: 0 
#> Thinning Rate: 1 
#> Number of Chains: 1 
#> Total Posterior Samples: 125 
#> 
#> Using the exponential spatial correlation model.
#> 
#> Using 5 nearest neighbors.
#> 
#> Source compiled with OpenMP support and model fit using 1 thread(s).
#> 
#> Adaptive Metropolis with target acceptance rate: 43.0
#> ----------------------------------------
#> 	Chain 1
#> ----------------------------------------
#> Sampling ... 
#> Batch: 1 of 5, 20.00%
#> 	Parameter	Acceptance	Tuning
#> 	beta[1]		4.0		0.98020
#> 	beta[2]		0.0		0.98020
#> 	beta[3]		0.0		0.98020
#> 	beta[4]		12.0		0.98020
#> 	phi		20.0		0.98020
#> -------------------------------------------------
#> Batch: 2 of 5, 40.00%
#> 	Parameter	Acceptance	Tuning
#> 	beta[1]		4.0		0.97045
#> 	beta[2]		4.0		0.97045
#> 	beta[3]		4.0		0.97045
#> 	beta[4]		4.0		0.97045
#> 	phi		8.0		0.97045
#> -------------------------------------------------
#> Batch: 3 of 5, 60.00%
#> 	Parameter	Acceptance	Tuning
#> 	beta[1]		8.0		0.96079
#> 	beta[2]		0.0		0.96079
#> 	beta[3]		4.0		0.96079
#> 	beta[4]		8.0		0.96079
#> 	phi		20.0		0.96079
#> -------------------------------------------------
#> Batch: 4 of 5, 80.00%
#> 	Parameter	Acceptance	Tuning
#> 	beta[1]		0.0		0.95123
#> 	beta[2]		0.0		0.95123
#> 	beta[3]		0.0		0.95123
#> 	beta[4]		4.0		0.95123
#> 	phi		32.0		0.95123
#> -------------------------------------------------
#> Batch: 5 of 5, 100.00%

# Predict at new locations ------------------------------------------------
colnames(X.0) <- c('intercept', 'abund.cov', 'abund.cov.2', 'abund.cov.3')
out.pred <- predict(out, X.0, coords.0)
#> ----------------------------------------
#> 	Prediction description
#> ----------------------------------------
#> NNGP spatial GLMM fit with 169 observations.
#> 
#> Number of covariates 4 (including intercept if specified).
#> 
#> Number of spatially-varying coefficients: 1 (including intercept if specified).
#> 
#> Using the exponential spatial correlation model.
#> 
#> Using 5 nearest neighbors.
#> 
#> Number of MCMC samples 125.
#> 
#> Predicting at 56 locations.
#> 
#> Source compiled with OpenMP support and model fit using 1 threads.
#> -------------------------------------------------
#> 		Predicting
#> -------------------------------------------------
#> Location: 56 of 56, 100.00%
#> Generating abundance predictions
mu.0.quants <- apply(out.pred$mu.0.samples, 2, quantile, c(0.025, 0.5, 0.975))
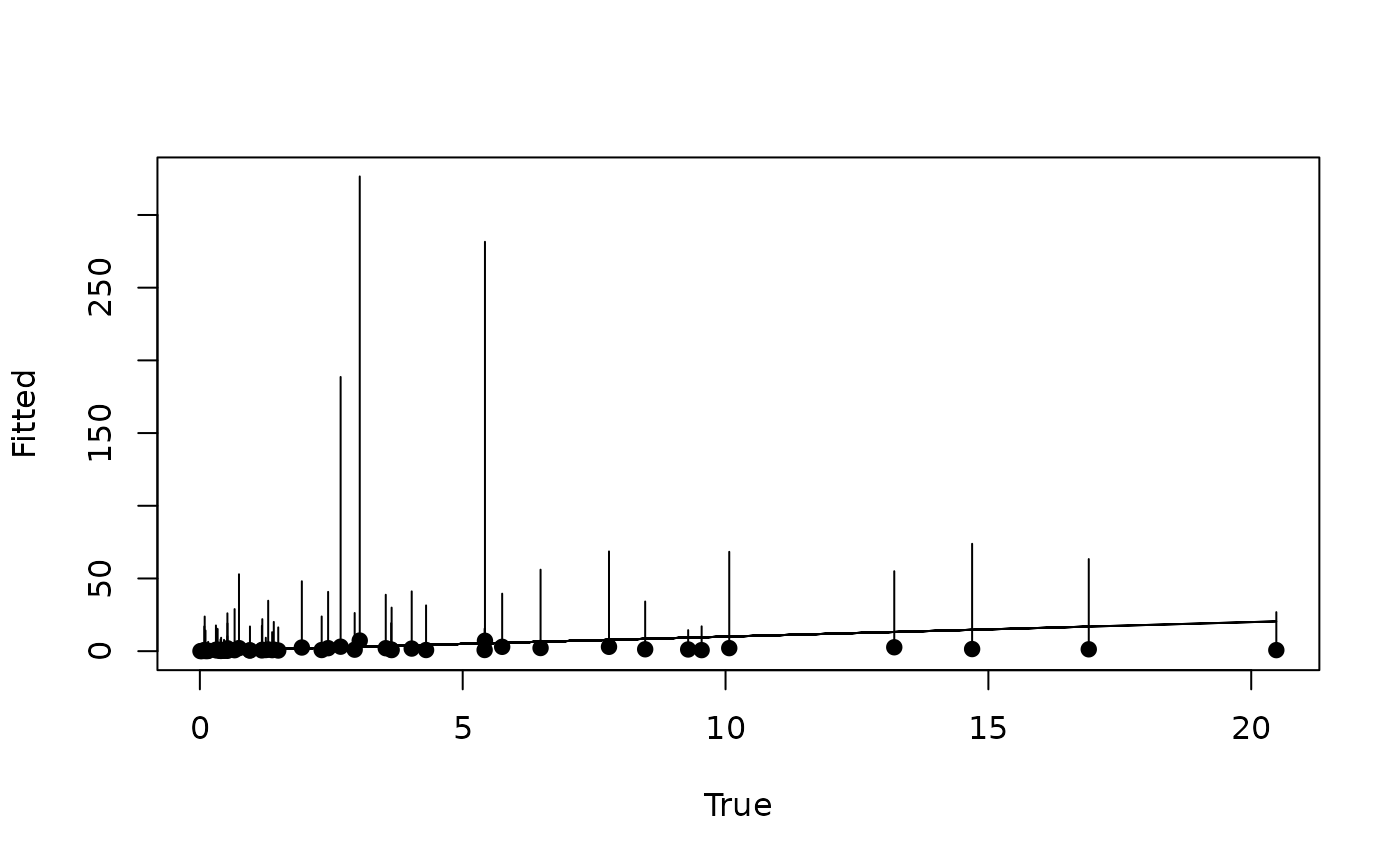
plot(dat$mu[pred.indx], mu.0.quants[2, ], pch = 19, xlab = 'True', 
     ylab = 'Fitted', ylim = c(min(mu.0.quants), max(mu.0.quants)))
segments(dat$mu[pred.indx], mu.0.quants[1, ], dat$mu[pred.indx], mu.0.quants[3, ])
lines(dat$mu[pred.indx], dat$mu[pred.indx])