
Convergence diagnostics and other considerations when fitting spatial occupancy models
Jeffrey W. Doser
2023 (last update: March 25, 2024)
Source:vignettes/modelConsiderations.Rmd
modelConsiderations.RmdIntroduction
In this article, I discuss issues related to convergence,
identifiability, and priors in spatially-explicit models fit in
spOccupancy. I come at these topics from a practical
perspective, focusing on the implications of identifiability and
convergence issues for researchers interested in fitting such models in
spOccupancy. Identifiability of parameters in Bayesian
analysis is a very wide-ranging and complex area of study, and this
article is not intended to assess identifiability of these models in a
formal statistical manner. For an interesting starting point on
identifiability in Bayesian analysis (and a variety of references
mentioned throughout), I encourage you to take a look at this
blog post from Andrew Gelman, as well as the discussion that follows
the original post. I have also provided a variety of references
throughout to the statistical literature that discuss identifiability in
factor models from a much more rigorous perspective.
This document is intended to be updated with additional guidance and
information on some of the more finicky parts of fitting the
spatially-explicit models available in spOccupancy. Much of
this document focuses on spatial factor occupancy models (i.e.,
spatially-explicit joint species distribution models with imperfect
detection), some of which comes from Appendix S3 in our
open access paper on spatial factor multi-species occupancy models
(Doser, Finley, and Banerjee (2023)).
However, I also address topics (i.e., choices of priors on spatial
parameters) that are relevant for spatially-varying coefficient
occupancy models and spatial occupancy models.
Specifying the prior for the spatial decay parameter \(\phi\) in spatial occupancy models
The prior on the spatial decay parameter \(\phi\) in all forms of spatial occupancy
models can be essential for adequate convergence of the model. Recall
that the spatial decay parameter \(\phi\) controls the range of the spatial
dependence. For the exponential correlation model, the spatial decay
parameter \(\phi\) has a nice
interpretation in that \(\frac{3}{\phi}\) is the effective
spatial range. The effective spatial range is defined as the
distance between sites at which the spatial autocorrelation falls to a
small value (0.05), and thus can be interpreted as how far across space
the spatial autocorrelation between two sites goes. From an ecological
perspective, this is a fairly intuitive parameter that can be related to
a lot of interesting processes such as the dispersal distance of the
species you’re working with, the underlying spatial pattern of any
missing covariates that are not included in the model, or a result of
the specific study design chosen (e.g., if sites are collected in a
cluster sampling design). However, in the type of spatial models we fit
in spOccupancy (i.e., point-referenced spatial models), the
spatial decay parameter \(\phi\) and
the spatial variance parameter \(\sigma^2\) (which controls the
magnitude of the spatial variability) are only weakly
identifiable. Theoretical work shows the product of the two parameters
is identifiable, but that the two parameters individually are only
weakly identifiable (H. Zhang 2004). This
is related to the intuitive idea that without any additional
information, our model would not be able to distinguish between very
fine-scale (i.e., small effective range, high \(\phi\)) spatial variability with a small
spatial variance and very broad-scale spatial variability (i.e., high
effective range, small \(\phi\)) with
low-magnitude spatial variance. Without going into the statistical
details, this means that our priors can have an important influence on
the resulting values of these two parameters. These problems are even
more prominent when working with binary data like we do in occupancy
models compared to working with continuous, Gaussian data for which most
of the theoretical statistical work regarding these models has been
developed. This is generally why I recommend against heavily
interpreting the estimates of these two parameters (\(\phi\) and \(\sigma^2\)) in single-season occupancy
models, in particular if working with a modest number of data points
(e.g., < 300). The additional information provided by sampling over
multiple seasons in multi-season occupancy models aids in estimation of
these parameters, and thus slightly more weight can be given to the
ecological interpretation of the parameters.
The importance of the priors (and specifically the prior on \(\phi\), which I discuss here) increases as
the model becomes complex. More specifically, the prior will be least
important for a basic single-species spatial occupancy model, but will
often be very important for spatially-varying coefficient occupancy
models as well as spatial factor multi-species occupancy models. Our
default prior that we place on the spatial decay parameter is
Uniform(\(3 / \text{max(dists)}\),
\(3 / \text{min(dists)}\)), where dists
represents the matrix of inter-site distances between all sites in the
data set. When thinking about what this means for an exponential
correlation function (which is also the default function in
spOccupancy), this means that our prior allows the
effective spatial range to be anywhere from the maximum inter-site
distance (i.e., broad-scale relative to the study area) to the minimum
inter-site distance (i.e., extremely fine-scale relative to the
distances between sites). This is quite an uninformative prior, because
we essentially are telling the model to determine whether the spatial
autocorrelation is large or fine scale only based on the patterns that
occur in the data.
While this prior typically works for basic single-species spatial
occupancy models (i.e., spPGOcc()) and often works for
other more complex models in spOccupancy, it can in some
instances lead to problems. In these cases, we may need to use a more
informative prior on the spatial decay parameter. When using an
exponential correlation model, doing this is relatively intuitive given
the interpretation of the effective spatial range as described in the
previous paragraph. Below I present a few scenarios in cases where it
may be useful to specify a more informative prior on \(\phi\) than what spOccupancy
does by default. This is certainly not an exhaustive list, but is meant
to give a flavor of some ways in which more informative priors are
useful/necessary to achieve convergence of a spatially-explicit model in
spOccupancy based on my own experiences fitting these
models, and problems that I’ve seen users have.
-
Cluster sampling design: consider the case where
detection-nondetection data are obtained at multiple points along a
transect, and each of these points along the transect is treated as a
site in the occupancy model. In such a case, we may want to put a
slightly more informative prior on \(\phi\) that reflects the design of the
study by ensuring the effective spatial range is at least as large as
the length of the transects. So, instead of setting the upper bound of
the uniform prior of \(\phi\) to \(3 / \text{min(dists)}\), in this scenario
we could set it to \(3 / \text{Transect
Length}\). This will ensure we inherently account for the
structure of the survey by ensuring the effective spatial range is at
least as large as the length of a transect. This is particularly
important in situations where sites within a transect are very close
together relative to the full spatial extent of the study region. See
Bajcz et al. (2024) for an example of
using an informative prior with
spOccupancywhen data were collected in a clustered design (e.g., multiple points were sampled within a lake, multiple lakes were sampled across a region). -
Spatially-varying coefficient occupancy models: for
both single-species and multi-species spatially-varying coefficient
occupancy models, one may encounter overfitting, such that the resulting
spatially-varying coefficient (SVC) estimates are extremely fine scale
and do not make much ecological sense. The flexibility of these models
is what makes them great in the sense that they can reveal very
interesting patterns in the spatial variation of species-environment
relationships and/or occupancy trends. However, this flexibility also
means that these models can be prone to overfitting. If using the
default priors for the spatial decay parameters with SVC models
(particularly SVC models with a fairly small number of spatial locations
(e.g., < 500 or so)), you may need to increase the lower bound of the
effective spatial range to avoid massive overfitting to the data.
Remember that in order to set a larger lower bound on the
effective spatial range of the spatial variation, you will need to
modify the upper bound of the prior on \(\phi\) (since they are inversely
correlated). Specifying exactly how to do this is somewhat dependent on
the specific data set and objectives of the study. This upper bound
could perhaps be determined based on the ecology of the species you’re
working with. For example, the modified upper bound of the spatial decay
parameter’s prior could be based on the home range or dispersal distance
of the species you are working with. Alternatively, it can be based on
the type of inference you want to draw from the model. If you are
interested in determining if there is support for broad-scale
variability in a species-environment relationship, this upper bound of
\(\phi\) can be set to something like
\(3 / \text{quantile(dists, 0.4)}\),
which is equivalent to saying the effective spatial range is at least as
large as the 40% quantile of the inter-site distances between the data
points. Such a prior would allow you to explore if there is any support
for medium to large-scale variation in the covariate effect.
Alternatively, for more fine-scale variability, you could use a lower
quantile of the inter-site distance matrix, so something like
quantile(dists, 0.1). How “fine-scale” this is will depend on the specific orientation of the spatial coordinates in a given data set, so again it may be better to specify a specific distance that represents fine-scale variation across the study region in which you’re working. Overall, SVC models are very flexible, but can also be too flexible in the sense that they are prone to overfitting, so careful consideration of the priors is more important for such models. I suggest first fitting an SVC model with the default prior for the spatial decay parameters, which is relatively uninformative. In some cases when overfitting is occurring, you may see this model fail to converge, in which case you may want to further restrict the upper bound of \(\phi\). In other cases, the model will converge, but after examining the SVC estimates it is clear that overfitting is occurring (e.g., the map of SVCs across spatial locations looks more like white noise than a spatially smooth pattern). In such cases, restricting the upper bound of the uniform prior on \(\phi\) can be important for using SVC models to test/generate hypotheses regarding the drivers of spatial variability in species-environment relationships and/or occupancy trends. I talk about these concepts in much more detail in a separate vignette. - Lack of convergence: in some cases the default prior is not informative enough to yield convergence of the model, and you may see the estimates of \(\phi\) (and also \(\sigma^2\) in the opposite way) flip back and forth between high values (e.g., small effective range) and low values (e.g., high effective range). In such cases, you will likely need to restrict the prior for \(\phi\) to estimate more large-range spatial autocorrelation (i.e., restrict the upper bound of the uniform prior for \(\phi\)) or to estimate more local-scale spatial autocorrelation (i.e., restrict the lower bound of the uniform prior for \(\phi\)). Again, this can be accomplished by using some quantiles of the intersite distance matrix, or by choosing specific distance values that make sense based on the spatial extent of the study region. I will point out that while spatial occupancy models can accommodate pretty fine-scale spatial autocorrelation, they are limited in their ability to estimate extremely fine-scale spatial variability. This is related to the fact that as the effective spatial range decreases towards zero, the spatial correlation in the spatial random effects occurs over a smaller distance, and thus the estimate of the spatial random effect at any given location is informed by a smaller number of data points and eventually becomes an unstructured site-level random effect. For binary data, it is not possible to estimate an unstructured site-level random effect (Bolker 2022). Thus, in some cases, we may by necessity have to restrict the upper bound of \(\phi\) to ensure the model does not get “stuck” at extremely small effective spatial range estimates which essentially lead to an unidentifiable model.
In conclusion, this section is meant to give some insight as to when, how, and why it may be useful to specify a more informative prior on \(\phi\). I’ll close by saying that while placing such restrictions on the spatial decay parameter can seem somewhat arbitrary, other approaches for estimating spatial autocorrelation (i.e., maximum likelihood approaches) and/or spatially-varying coefficients (e.g., geographically weighted regression) fix the effective spatial range prior to fitting the model. In general, specifying potentially informative priors on \(\phi\) while exploring different levels of information included in the prior is a robust way to ensuring the model is identifiable, allows us to answer the questions we’re interested in, and allows us to explore the impacts our priors have on the resulting estimates (e.g., via sensitivity analyses).
Choosing the number of latent factors in spatial factor models
Determining the number of latent factors to include in a spatial factor multi-species occupancy model or non-spatial latent factor multi-species occupancy model is not straightforward. Often using as few as 2-5 factors is sufficient, but for particularly large communities (e.g., \(N = 600\)), a larger number of factors may be necessary to accurately represent variability among the species (Tobler et al. 2019; Tikhonov et al. 2020). While other approaches exist to estimate the “optimal” number of factors directly in the modeling framework (Tikhonov et al. 2020), these approaches do not allow for interpretability of the latent factors and the latent factor loadings. The specific restraints and priors we place on the factor loadings matrix (\(\boldsymbol{\Lambda}\)) in our approach allows for interpretation of the latent factors and the factor loadings, but does not automatically determine the number of factors for optimal predictive performance. Thus, there is a trade-off between interpretability of the latent factors and factor loadings and optimal predictive performance. In our implementation, we chose to allow for interpretability of the factor and factor loadings at risk of inferior predictive performance if too many or too few factors are specified by the user.
The number of latent factors can range from 1 to \(N\) (the total number of species in the modeled community). Conceptually, choosing the number of factors is similar to performing a principal components analysis and looking at which components explain a large amount of variation. We want to choose the number of factors that explains an adequate amount of variability among species in the community, but we want to keep this number as small as possible to avoid overfitting the model and large model run times. When initially specifying the number of factors, we suggest the following:
- Consider the size of the community and how much variation there is between species. If there is expected large variation in occurrence patterns for all species in the community, the user may require a larger number of factors. If the modeled community is comprised of certain groups of species that are expected to behave similarly (e.g., insectivores, frugivores, granivores), then a smaller number of factors may suffice. Further, as shown by Tikhonov et al. (2020), as the number of species increases, more factors will likely be necessary to adequately represent variability in the community.
- Consider the amount of computational time/power that is available. Model run time to achieve convergence will increase as more factors are included in the model. Under certain circumstances (i.e., there is a large number of spatial locations in the data set), reasonal run times may only be possible with a modest or small number of factors.
- Consider the rarity of species in the community, how many spatial locations (i.e., sites) are in the data set, and how many replicates are available at each site. Models with more latent factors have more parameters to estimate, and thus require more data. If there are large numbers of rare species in the community, we may be limited in the number of factors we can specify in the model, as models with more than a few factors may not be identifiable. Such a problem may also arise when working with a small number of spatial locations (e.g., 30 sites) or replicates (e.g., 1 or 2 replicates at each site).
Convergence Assessment of Spatial Factor Models (and other spatial occupancy models)
Spatial (and non-spatial) factor models can be difficult to fit,
requiring a large number of MCMC samples and fairly long run times
(e.g., hours or days), even with the computational advancements
implemented in spOccupancy. Further, assessing convergence
in spatial factor models can be a complicated task. These models include
multiple levels of latent variables that we are trying to estimate:
multiple spatial NNGPs (i.e., the spatial factors) along with their
associated species-specific coefficients (factor loadings) are estimated
to accommodate residual correlations and spatial autocorrelation, and
the estimated occupancy values themselves are a (partially observed)
latent state that we need to disentangle from the imperfect detection
process. Trying to do all of this with a set of binary data points
(i.e., the detection-nondetection data) can be a difficult task,
especially when there is not an extremely large number of spatial
locations or there are a lot of rare species in the data set. Given the
complexity of these models, and the somewhat “weak identifiability” of
some of the model parameters (particularly those associated with the
spatial autocorrelation), the default convergence criteria that are
presented when running the summary() function in
spOccupancy may not provide the whole picture as to whether
or not the “model has converged”. In the following, we elaborate on
different convergence/identifiability issues that may arise when fitting
spatial factor models. We first start off with a discussion of an
“initial convergence assessment”, which is what we recommend doing for
all models in spOccupancy. If adequate time has been spent
in this portion of the assessment and some issues are still arising, the
additional identifiability and convergence issues discussed later in the
document can be helpful for diagnosing problems, and/or determining if
you can proceed with the objectives of your analysis (or if the model is
too complicated to be fit with your data).
Initial convergence assessment
In some situations, particularly when working with a large data set, not too many rare species, and only a few factors in the spatial factor model, the usual convergence criteria (i.e., visual assessment of traceplots, effective sample sizes, Gelman-Rubin Rhat diagnostic) can be used to assess convergence, and they will show adequate convergence of all model parameters. There are plenty of much more in-depth resources available for discussing convergence in MCMC-based Bayesian models, and what we present here is by no-means an all inclusive discussion of how to assess convergence. While we recommend the following approach, this does not mean that other methods of convergence assessment are not useful for providing additional evidence of convergence.
Here, we make use of three tools for this initial convergence assessment:
- Gelman-Rubin Rhat diagnostic
- Effective Sample Size
- Visual assessment of trace plots
Let’s consider a simulated data set with 7 species, 225 spatial
locations, 1 latent factor, and 3 replicate surveys at each site. Below
we simulate the data set with simMsOcc() and run a model
using sfMsPGOcc() with 3 chains (remember that Rhat
requires fitting multiple chains with different starting values). Note
that in this vignette we assume you have familiarity with
spOccupancy syntax. If not, I encourage you to check out the
introductory vignette.
# So we can get the same results.
set.seed(222901)
library(spOccupancy)
library(coda)
# Simulate Data -----------------------------------------------------------
J.x <- 15
J.y <- 15
J <- J.x * J.y
n.rep <- rep(3, J)
N <- 7
beta.mean <- c(0, 0.5)
p.occ <- length(beta.mean)
tau.sq.beta <- c(1, 1.5)
alpha.mean <- c(0, 1.2)
tau.sq.alpha <- c(1, 0.5)
p.det <- length(alpha.mean)
psi.RE <- list()
p.RE <- list()
beta <- matrix(NA, nrow = N, ncol = p.occ)
alpha <- matrix(NA, nrow = N, ncol = p.det)
for (i in 1:p.occ) {
beta[, i] <- rnorm(N, beta.mean[i], sqrt(tau.sq.beta[i]))
}
for (i in 1:p.det) {
alpha[, i] <- rnorm(N, alpha.mean[i], sqrt(tau.sq.alpha[i]))
}
n.factors <- 1
alpha.true <- alpha
phi <- 3 / 0.5
dat <- simMsOcc(J.x = J.x, J.y = J.y, n.rep = n.rep, N = N, beta = beta, alpha = alpha,
psi.RE = psi.RE, p.RE = p.RE, phi = phi, sp = TRUE,
cov.model = 'exponential', n.factors = n.factors, factor.model = TRUE)
# Number of batches
n.batch <- 400
# Batch length
batch.length <- 25
n.samples <- n.batch * batch.length
n.burn <- 4000
n.thin <- 3
n.chains <- 3
y <- dat$y
X <- dat$X
X.p <- dat$X.p
X.p.re <- dat$X.p.re
X.p.re <- dat$X.p.re + 10
coords <- dat$coords
occ.covs <- cbind(X)
colnames(occ.covs) <- c('int', 'occ.cov.1')
det.covs <- list(det.cov.1 = X.p[, , 2])
data.list <- list(y = y, coords = coords, occ.covs = occ.covs,
det.covs = det.covs)
# Priors
prior.list <- list(beta.comm.normal = list(mean = 0, var = 2.72),
alpha.comm.normal = list(mean = 0, var = 2.72),
tau.sq.beta.ig = list(a = 0.1, b = 0.1),
tau.sq.alpha.ig = list(a = 0.1, b = 0.1))
out <- sfMsPGOcc(occ.formula = ~ occ.cov.1,
det.formula = ~ det.cov.1,
data = data.list,
n.batch = n.batch,
n.factors = n.factors,
batch.length = batch.length,
accept.rate = 0.43,
priors = prior.list,
cov.model = "exponential",
n.omp.threads = 1,
verbose = TRUE,
NNGP = TRUE,
n.neighbors = 5,
search.type = 'cb',
n.report = 100,
n.burn = n.burn,
n.thin = n.thin,
n.chains = n.chains)----------------------------------------
Preparing to run the model
----------------------------------------No prior specified for phi.unif.
Setting uniform bounds based on the range of observed spatial coordinates.z is not specified in initial values.
Setting initial values based on observed databeta.comm is not specified in initial values.
Setting initial values to random values from the prior distributionalpha.comm is not specified in initial values.
Setting initial values to random values from the prior distributiontau.sq.beta is not specified in initial values.
Setting initial values to random values between 0.5 and 10tau.sq.alpha is not specified in initial values.
Setting initial values to random values between 0.5 and 10beta is not specified in initial values.
Setting initial values to random values from the community-level normal distributionalpha is not specified in initial values.
Setting initial values to random values from the community-level normal distributionphi is not specified in initial values.
Setting initial value to random values from the prior distributionlambda is not specified in initial values.
Setting initial values of the lower triangle to 0----------------------------------------
Building the neighbor list
----------------------------------------
----------------------------------------
Building the neighbors of neighbors list
----------------------------------------
----------------------------------------
Model description
----------------------------------------
Spatial Factor NNGP Multi-species Occupancy Model with Polya-Gamma latent
variable fit with 225 sites and 7 species.
Samples per chain: 10000 (400 batches of length 25)
Burn-in: 4000
Thinning Rate: 3
Number of Chains: 3
Total Posterior Samples: 6000
Using the exponential spatial correlation model.
Using 1 latent spatial factors.
Using 5 nearest neighbors.
Source compiled with OpenMP support and model fit using 1 thread(s).
Adaptive Metropolis with target acceptance rate: 43.0
----------------------------------------
Chain 1
----------------------------------------
Sampling ...
Batch: 100 of 400, 25.00%
Latent Factor Parameter Acceptance Tuning
1 phi 36.0 0.56553
-------------------------------------------------
Batch: 200 of 400, 50.00%
Latent Factor Parameter Acceptance Tuning
1 phi 52.0 0.54335
-------------------------------------------------
Batch: 300 of 400, 75.00%
Latent Factor Parameter Acceptance Tuning
1 phi 44.0 0.52205
-------------------------------------------------
Batch: 400 of 400, 100.00%
----------------------------------------
Chain 2
----------------------------------------
Sampling ...
Batch: 100 of 400, 25.00%
Latent Factor Parameter Acceptance Tuning
1 phi 40.0 0.49164
-------------------------------------------------
Batch: 200 of 400, 50.00%
Latent Factor Parameter Acceptance Tuning
1 phi 40.0 0.48191
-------------------------------------------------
Batch: 300 of 400, 75.00%
Latent Factor Parameter Acceptance Tuning
1 phi 60.0 0.51171
-------------------------------------------------
Batch: 400 of 400, 100.00%
----------------------------------------
Chain 3
----------------------------------------
Sampling ...
Batch: 100 of 400, 25.00%
Latent Factor Parameter Acceptance Tuning
1 phi 36.0 0.49164
-------------------------------------------------
Batch: 200 of 400, 50.00%
Latent Factor Parameter Acceptance Tuning
1 phi 36.0 0.49164
-------------------------------------------------
Batch: 300 of 400, 75.00%
Latent Factor Parameter Acceptance Tuning
1 phi 32.0 0.51171
-------------------------------------------------
Batch: 400 of 400, 100.00%The summary() function provides the Rhat and effective
sample size (ESS) for many of the model parameters. We can start to
assess convergence with a quick call to summary() as done
below.
summary(out)
Call:
sfMsPGOcc(occ.formula = ~occ.cov.1, det.formula = ~det.cov.1,
data = data.list, priors = prior.list, cov.model = "exponential",
NNGP = TRUE, n.neighbors = 5, search.type = "cb", n.factors = n.factors,
n.batch = n.batch, batch.length = batch.length, accept.rate = 0.43,
n.omp.threads = 1, verbose = TRUE, n.report = 100, n.burn = n.burn,
n.thin = n.thin, n.chains = n.chains)
Samples per Chain: 10000
Burn-in: 4000
Thinning Rate: 3
Number of Chains: 3
Total Posterior Samples: 6000
Run Time (min): 0.8452
----------------------------------------
Community Level
----------------------------------------
Occurrence Means (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) -0.7853 0.3303 -1.3430 -0.8161 -0.0239 1.0058 1317
occ.cov.1 0.5019 0.5612 -0.6171 0.5051 1.6284 1.0010 5225
Occurrence Variances (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) 0.6703 0.8831 0.0629 0.4112 2.8789 1.0128 601
occ.cov.1 2.6129 2.2852 0.6621 1.9823 8.4035 1.0036 4347
Detection Means (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) -0.2413 0.4547 -1.1608 -0.2367 0.6539 1.0006 6000
det.cov.1 0.9647 0.3415 0.2532 0.9701 1.6427 1.0003 6000
Detection Variances (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) 1.5501 1.2922 0.4278 1.1887 4.9658 1.0054 5531
det.cov.1 0.8544 0.8469 0.2082 0.6302 2.8713 1.0012 5176
----------------------------------------
Species Level
----------------------------------------
Occurrence (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept)-sp1 -1.2406 0.3180 -1.9335 -1.2193 -0.6746 1.0143 270
(Intercept)-sp2 0.0753 0.6256 -0.8977 -0.0038 1.4843 1.0332 303
(Intercept)-sp3 -0.6740 0.2075 -1.0866 -0.6726 -0.2771 1.0020 3153
(Intercept)-sp4 -1.4734 0.3148 -2.1186 -1.4635 -0.8891 1.0427 407
(Intercept)-sp5 -0.9467 0.1901 -1.3226 -0.9479 -0.5756 1.0026 1723
(Intercept)-sp6 -0.3234 0.5771 -1.3008 -0.3796 0.9638 1.0173 159
(Intercept)-sp7 -1.0868 0.2436 -1.5779 -1.0829 -0.6120 1.0099 392
occ.cov.1-sp1 -0.8358 0.2070 -1.2605 -0.8294 -0.4454 1.0002 4291
occ.cov.1-sp2 1.6407 0.6337 0.6574 1.5473 3.1646 1.0135 277
occ.cov.1-sp3 2.7640 0.4166 2.0416 2.7362 3.6734 1.0132 1848
occ.cov.1-sp4 -0.7524 0.2175 -1.1988 -0.7474 -0.3535 1.0019 3903
occ.cov.1-sp5 0.5806 0.1836 0.2341 0.5750 0.9621 1.0015 5108
occ.cov.1-sp6 -0.3339 0.2840 -0.9235 -0.3260 0.2032 1.0038 2471
occ.cov.1-sp7 0.7874 0.1941 0.4273 0.7792 1.1889 1.0006 4591
Detection (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept)-sp1 -0.3043 0.2150 -0.7240 -0.3010 0.1152 1.0019 3026
(Intercept)-sp2 -2.0115 0.2827 -2.5421 -2.0144 -1.4475 1.0268 475
(Intercept)-sp3 1.2041 0.1600 0.8920 1.2011 1.5227 1.0043 5239
(Intercept)-sp4 -0.4705 0.2575 -0.9877 -0.4610 0.0214 1.0131 2797
(Intercept)-sp5 -0.1973 0.2007 -0.5961 -0.1960 0.1975 1.0007 4564
(Intercept)-sp6 -0.6475 0.1763 -0.9906 -0.6475 -0.3066 1.0000 3838
(Intercept)-sp7 0.6612 0.1871 0.2985 0.6572 1.0326 1.0017 4744
det.cov.1-sp1 1.2438 0.2249 0.8179 1.2364 1.7073 0.9999 5160
det.cov.1-sp2 0.5774 0.1882 0.2165 0.5724 0.9710 1.0055 4146
det.cov.1-sp3 0.2816 0.1540 -0.0164 0.2808 0.5937 1.0011 6000
det.cov.1-sp4 0.3142 0.1964 -0.0545 0.3090 0.7117 1.0001 6000
det.cov.1-sp5 1.2314 0.2266 0.8059 1.2223 1.6956 1.0043 4932
det.cov.1-sp6 2.3649 0.2776 1.8482 2.3522 2.9453 1.0096 2519
det.cov.1-sp7 1.0562 0.1924 0.6820 1.0515 1.4448 1.0013 5435
----------------------------------------
Spatial Covariance
----------------------------------------
Mean SD 2.5% 50% 97.5% Rhat ESS
phi-1 5.9866 2.0527 2.5679 5.8311 10.6453 1.0048 319The last two columns contain the Rhat and ESS values. A general rule
of thumb is that convergence has occurred when Rhat values are less than
1.1. The foundational principle of Rhat is that it compares the
variation of parameter estimates among chains with different
starting values to the variation of parameters within chains
(fundamentally similar to an ANOVA). If this ratio (among
variance/within variance) is close to 1, this suggests the chains have
converged to the true posterior distribution. In this example, we see
all Rhat values presented are less than 1.1, indicating good convergence
of the model. While the parameters shown in the summary()
output are not all the parameters estimated in the model, we have found
that convergence of other parameters not shown here (e.g., the factor
loadings, factors, and latent occupancy values) consistently follows the
parameters included in the summary, such that if the parameters in the
summary have converged, so have the other parameters. If interpreting
the latent factors and factor loadings, we do suggest also checking the
convergence of the factor loadings as well, which are in the
out$lambda.samples component of the model. We can access
the Rhat and ESS values for the factor loadings with the following:
out$ESS$lambda sp1-1 sp2-1 sp3-1 sp4-1 sp5-1 sp6-1 sp7-1
0.0000 450.6036 2741.7868 2209.1605 2753.0260 916.6525 2064.5254
out$rhat$lambda.lower.tri[1] 1.025019 1.002586 1.001293 1.009842 1.006515 1.009461Note the Rhat for the factor loadings is only reported for the components of the matrix in the lower triangle, since these are the only parameters that are estimated.
Additionally, the ESS values for all parameters are “substantially large”. There is no “one size fits all” cutoff for what indicates a “good” ESS, as it depends on the objective of the study, how complicated the model is, and how much degree of Monte Carlo error you’re willing to accept in your estimates. ESS values that are low (e.g., 100 or less), together with Rhat values close to or above 1.1 can indicate inadequate convergence and/or mixing of the MCMC chains, in which case one may want to run the model longer. Generally when fitting spatial occupancy models, the detection parameters will mix and converge faster than the occupancy parameters (assuming an adequate amount of replication to separate occupancy from detection, which may not be true with a very small number of replicates). In particular, the spatial decay parameters and the occupancy intercepts may show slow mixing and/or convergence, which I discuss more in depth below as to what to do in this case.
In addition to using the Rhat and ESS values presented by the
summary() output, we strongly suggest further exploration
of the MCMC chains via visual inspection of traceplots. While Rhat and
ESS are effective summaries that provide a good indication of the
convergence (i.e., Rhat) and mixing (i.e., ESS) of the models, they are
of course summarizing a full posterior distribution with a single
numeric value, and thus visual assessments will also be of use. In the
fitted model object (here saved as out), the list
components that end in samples contain the MCMC samples for
the different parameters in the model. Many of these objects are saved
as MCMC objects, so we can directly use coda::plot() or
other functions to generate traceplots of the MCMC chains. For the MCMC
parameters that are stored as three-dimensional arrays (e.g., the latent
occurrence values), you’ll need to plot only two dimensions at a time
using the basic coda functionality.
# Species-specific intercepts
plot(out$beta.samples[, 1:7], density = FALSE)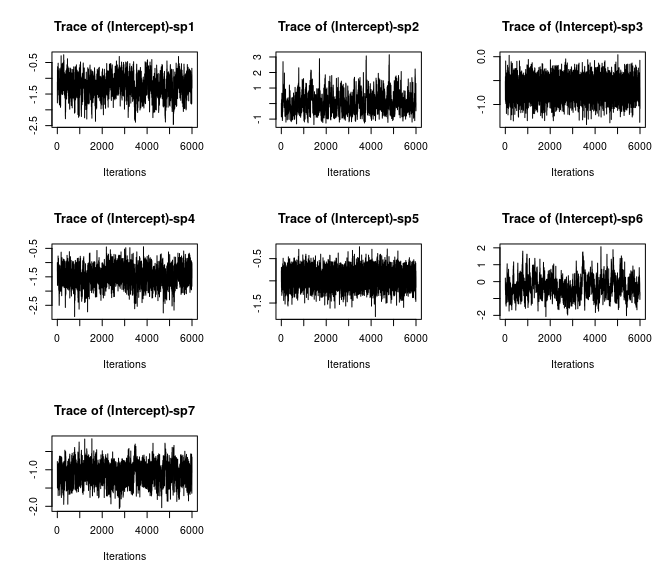
# Species-specific covariate effects
plot(out$beta.samples[, 8:14], density = FALSE)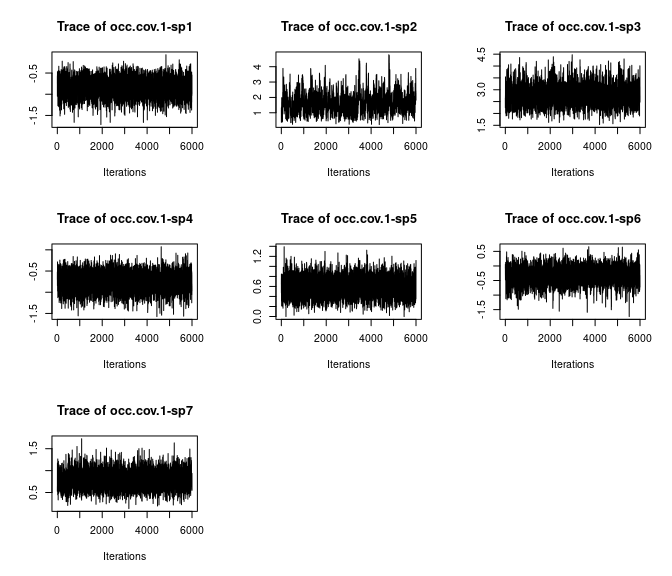
When running a model in spOccupancy with multiple
chains, the MCMC sampls from each chain will be appended to each other
in a single MCMC object rather than a list, which is why you don’t see
three chains plotted on top of each other in the corresponding plots.
This may not be ideal for visualization purposes, but it helps with
extraction and manipulation of the samples. In v0.7.2, I added in a
simple plot() function that allows you to quickly generate
traceplots where multiple chains are plotted on top of each other for
most parameters in a spOccupancy model object.
plot(out, 'lambda', density = FALSE)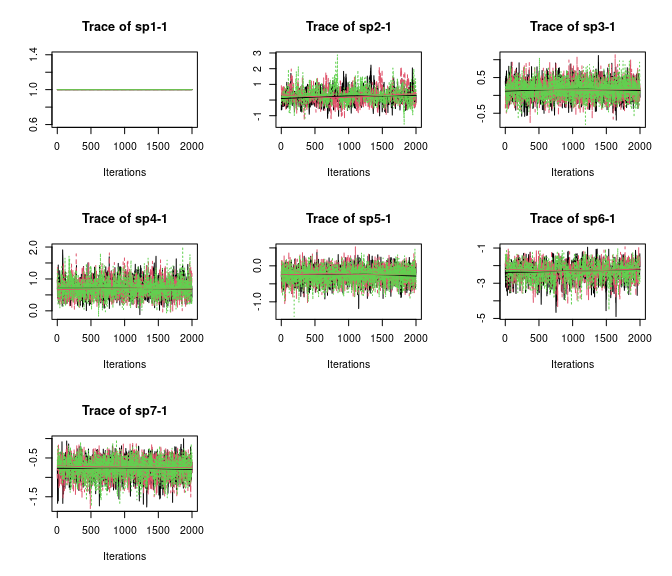
Here we see all species-specific intercept and covariate effects appear to have converged, with substantial variability in how well the chains have mixed for the different species. Generally, mixing appears better for the covariate effect than the intercept.
# Spatial decay parameter
plot(out, 'theta', density = FALSE)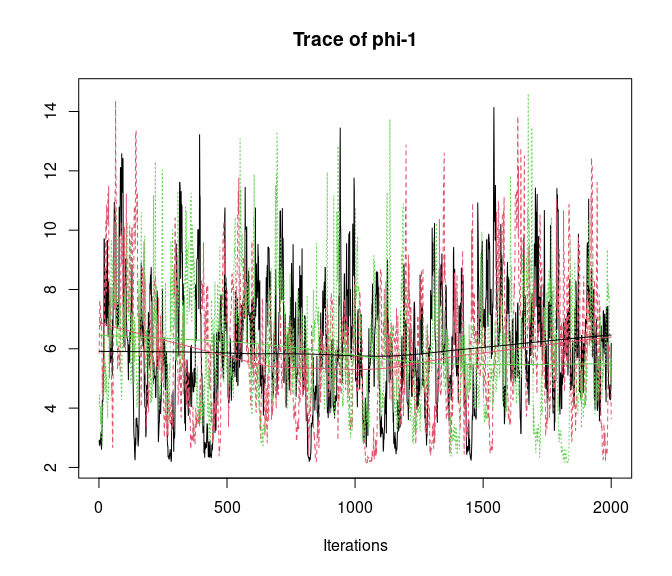
Overall, all Rhat values are less than 1.1, effective sample sizes are decently large for the model parameters, and the traceplots show convergence and good mixing for the parameters. We would consider this model suitably converged and move on with our analysis and interpretation of the results. If our objectives focused heavily on interpreting the species-specific intercepts and covariate effects (and particularly the uncertainty associated with them), we may run the chain a bit longer/save more posterior MCMC samples to increase our effective sample size and thus be more confident in the accuracy of our uncertainty measurements for these parameters.
This was an example where this initial convergence assessment, which generally mirrors standard practices in Bayesian MCMC based methods, shows a model that has suitably converged. However, in many cases with such complicated models we will see that our initial convergence assessment shows some sort of failure, whether it be extremely low effective sample sizes, high Rhat values, or weird-looking MCMC chains. In the following we discuss specific scenarios where such problems are common to arise in these models and provide suggestions as to how to proceed in these situations (beyond the usual recommendations of running more MCMC samples, increasing the burn-in, increasing the thinning rate).
Identifiability of the spatial factors, factor loadings, and species-specific intercepts in spatial factor models
One key problem you may encounter when fitting spatial factor
multi-species occupancy models is seemingly very different parameter
estimates across model fits with different starting values (i.e.,
different chains when using the n.chains argument), leading
to extremely high Rhat values and very low ESS values, even though
within a given chain the posteriors look as if they have converged and
adequately mixed. This sensitivity to initial values is primarily due to
difficulty in separately estimating the spatial factors from the factor
loadings. Let’s consider again the structure of the spatial factor
component of the model. Considering a model with a single covariate, we
model occupancy probability for each species \(i\) at each spatial location \(\boldsymbol{s}_j\) following
\[ \text{logit}(\boldsymbol{\psi}_i(\boldsymbol{s}_j) = \tilde{\beta}_{i, 0}(\boldsymbol{s}_j) + \beta_{i, 1} \cdot x_1(\boldsymbol{s}_j), \]
where \(\tilde{\beta}_{i, 0}(\boldsymbol{s}_j)\) is the species-specific intercept value at each spatial location, and \(\beta_{i, 1}\) is the species-specific covariate effect. The species-specific intercept is comprised of a non-spatial component and a spatial component following
\[ \begin{aligned} \tilde{\beta}_{i, 0}(\boldsymbol{s}_j) &= \beta_{i, 0} + \text{w}_i^\ast(\boldsymbol{s}_j) \\ &= \beta_{i, 0} + \boldsymbol{\lambda}_i^\top\textbf{w}(\boldsymbol{s}_j). \end{aligned} \]
We can see from this last equation that the species-specific intercept at each spatial location is composed of three unknown components that we are estimating: (1) \(\beta_{i, 0}\): the overall non-spatial intercept; (2) \(\boldsymbol{\lambda}_i\): the species-specific factor loadings; and (3) \(\textbf{w}(\boldsymbol{s}_j)\): the spatial factors at each spatial location. It is this decomposition of \(\tilde{\beta}_{1, 0}\) into these separate components that leads to seemingly large problems in convergence.
Consider the product \(\boldsymbol{\lambda}_i^\top\textbf{w}(\boldsymbol{s}_j)\),
which is the component related to the spatial factor model. Trying to
estimate this product can be thought of as estimating a missing
covariate (i.e., \(\textbf{w}(\boldsymbol{s}_j)\)) along with
the effects of that “covariate” on each species \(\boldsymbol{\lambda}_i\). The literature on
traditional factor models and their spatially-explicit equivalents
extensively discussess the separate identifiability of the factors and
loadings, which is not straightforward (Hogan and
Tchernis 2004; Ren and Banerjee 2013; L. Zhang and Banerjee 2022;
Papastamoulis and Ntzoufras 2022). In the approach we take in
spOccupancy, we fix values of the factor loadings matrix to
improve the separate identifiability of the loadings from the spatial
factors. Specifically, we fix the upper triangular elements to 0 and the
diagonal elements to 1. This approach generally provides separate
identifiability of the factor loadings and factors, allowing us to
visualize and interpret them and potentially provide us with information
on species clustering (Taylor-Rodriguez et al.
2019).
However, identifiability issues can still arise in specific circumstances when using this approach, leading to the values of the factor loadings and spatial factors being dependent on the initial starting values of the MCMC algorithm. This sensitivity to initial values arises because the model can be invariant to a switch in sign of the factor loadings and spatial factors. In other words, the model cannot distinguish between \(\boldsymbol{\lambda}_i^\top\textbf{w}(\boldsymbol{s}_j)\) and \((-\boldsymbol{\lambda}_i)^\top(-\textbf{w}(\boldsymbol{s}_j))\) (i.e., they are both equally valid “solutions” to the model). Thus, when running multiple chains of a model with drastically different starting values, which form of this product that the model converges upon will depend on the initial values. Our approach that fixes certain elements of the factor loadings matrix \(\boldsymbol{\Lambda}\) generally mitigates this problem, but it can still occur when one of the first \(q\) spatial factors does not load onto any factor (in other words, the estimated factor loadings for that given spatial factor are all close to zero; Papastamoulis and Ntzoufras (2022)).
From a practical perspective, this has a couple important implications. If fitting a spatial factor model and you see vastly different estimates in the factor loadings across different chains that individually appear to have converged, consider the following recommendations:
-
Carefully consider the order of the species: the
order of the first \(q\) species has
substantial implications for the resulting convergence and mixing of the
chains. Because of the restrictions we place on the factor loadings
matrix \(\boldsymbol{\Lambda}\)
(diagonal elements equal to 1 and upper triangle elements equal to 0),
we may also need to carefully consider the order of the first \(q\) species in the detection-nondetection
data array, as it is these species that will have restrictions on their
factor loadings. We have found that careful consideration of the
ordering of species can lead to (1) increased interpretability of the
factors and factor loadings; (2) faster model convergence; (3) improved
mixing, and (4) reduction in the sensitivity of model estimates to
initial values. Determining the order of the factors is less important
when there are an adequate number of observations for all species in the
community, but it becomes increasingly important as more rare species
are present in the data set. If an initial convergence assessment is
showing inadequate convergence of the factor loadings, we suggest the
following when considering the order of the species in the
detection-nondetection array:
- Place a common species first. The first species has all of its factor loadings set to fixed values, and so it can have a large influence on the resulting interpretation of the factor loadings and latent factors. We have also found that having a rare species first can result in slow mixing of the MCMC chains and increased sensitivity to initial values of the latent factor loadings matrix.
- For the remaining \(q - 1\) factors, place species that are a priori believed to show different occurrence patterns than the first species, as well as the other species placed before it. Place these remaining \(q - 1\) species in order of decreasing differences from the initial factor. For example, if we fit a spatial factor multi-species occupancy model with three latent factors (\(q = 3\)) and were encountering difficult convergence of the MCMC chains, for the second species in the array, we would place a species that we believed shows large differences in occurrence patterns from the first species. For the third species in the array, we would place a species that we believed to show different occurrence patterns than both the first and second species, but its patterns may not be as noticeably different compared to the differences between the first and second species.
- Adjust the species ordering after an initial fit of the model. If one of the first \(q\) species in the model (and particularly the first species) has little residual variation in occurrence probability after accounting for the covariates in the model, it may cause identifiability issues when estimating the factor loadings. This occurs when using our approach to yielding identifiability of the factor loadings and spatial factors because the \(r\)th factor loading for the \(r\)th species is fixed to 1, whereas if we could estimate this coefficient and there is no residual variation in occurrence probability for that species then it would likely be close to zero. To avoid this problem, Carvalho et al. (2008) recommends first fitting a factor model, then for the \(r\)th factor identify the species with the largest magnitude factor loading for that factor, and then put that species as the \(r\)th species in the detection-nondetection data array and refit the model. We have found this to be a useful approach when the aforementioned guidance is inadequate.
-
Only fit one chain for spatial factor models:
another alternative to avoid problems with sensitivity to initial values
as a result of sign-switching is to only run a single MCMC chain for a
given model and use alternative tools from the Rhat diagnostic to assess
convergence. This approach is used for many prominent R packages that
fit similar factor models (i.e.,
boral(Hui 2016) andMCMCpack(Park, Quinn, and Martin 2011)). When assessing convergence/mixing with one chain, you can still visually explore traceplots as before and look at the effective sample sizes. Further, there exist other numeric convergence criteria that can be used to assess convergence with a single chain. Perhaps most prominent is the Geweke diagnostic (Geweke 1992). This criterion essentially performs a t-test between the first and last part of a Markov chain. If the samples are drawn from the stationary posterior distribution, then the means should be essentially equal and the returned z-score should be between approximately 2 and -2. We can calculate this diagnostic with thecoda::geweke.diag()function. Below we calculate the diagnostic for the factor loadings parameters, using only the first 2000 samples from the first chain we ran.
geweke.diag(out$lambda.samples[1:2000, ])
Fraction in 1st window = 0.1
Fraction in 2nd window = 0.5
sp1-1 sp2-1 sp3-1 sp4-1 sp5-1 sp6-1 sp7-1
NaN -1.27593 -0.39445 -0.07970 0.01836 -1.58411 0.29453 Note the first value returns NaN, which happens since we fix the first factor loading to 1. All other values are between 2 and -2, suggesting convergence of the chain. Together with visual assessment of traceplots and ensuring adequate mixing using ESS, this is a completely valid way for assessing convergence and avoiding the sign “flip-flopping” that can occur when fitting factor models with multiple chains with disparate starting values.
- Consider using more factors: although estimating fewer spatial factors is generally an easier task than estimating a large number of factors (i.e., because it requires estimating less parameters), we have found the aforementioned chain “flip-flopping” problem can be particularly common when using far fewer factors than are needed for a specific community. In such a situation, we often see the chains flip-flopping between factors that represent completely different underlying spatial patterns, which can particularly happen if the order of the species is not great (see point 1 in this section). Thus, when encountering large amounts of “chain flip-flopping”, this can be indicative of using too few factors, and so trying to use a larger number of factors can often mitigate the problem. As mentioned previously, as the number (and variety) of species in the community increases, more factors will generally be needed to adequately account for residual spatial autocorrelation across the species.