
Introduction to spOccupancy
Jeffrey W. Doser, Andrew O. Finley, Marc Kéry, Elise F. Zipkin
2022 (last update: December 13, 2024)
Source:vignettes/modelFitting.Rmd
modelFitting.RmdIntroduction
This vignette provides worked examples and explanations for fitting
single-species, multi-species, and integrated occupancy models in the
spOccupancy R package. We will provide step by step
examples on how to fit the following models:
- Occupancy model using
PGOcc(). - Spatial occupancy model using
spPGOcc(). - Multi-species occupancy model using
msPGOcc(). - Spatial multi-species occupancy model using
spMsPGOcc(). - Integrated occupancy model using
intPGOcc(). - Spatial integrated occupancy model using
spIntPGOcc().
We fit all occupancy models using Pólya-Gamma data augmentation (Polson, Scott, and Windle 2013) for
computational efficiency (Pólya-Gamma
is where the PG comes from in all spOccupancy
model fitting function names). In this vignette, we will provide a brief
description of each model, with full statistical details provided in a
separate MCMC
sampler vignette. We will also show how spOccupancy
provides functions for posterior predictive checks as a Goodness of Fit
assessment, model comparison and assessment using the Widely Applicable
Information Criterion (WAIC), k-fold cross-validation, and out of sample
predictions using standard R helper functions (e.g.,
predict()).
Note that this vignette does not detail all spOccupancy
functionality, and rather just details the core functionality presented
in the original implementation of the package. Additional functionality,
and associated vignettes, include:
- Improved spatial multi-species occupancy models that account for residual species correlations
- Multi-season occupancy models
- Spatially-varying coefficient occupancy models
- Integrated multi-species occupancy models
To get started, we load the spOccupancy package, as well
as the coda package, which we will use for some MCMC
summary and diagnostics. We will also use the stars and
ggplot2 packages to create some basic plots of our results.
We then set a seed so you can reproduce the same results as we do.
Example data set: Foliage-gleaning birds at Hubbard Brook
As an example data set throughout this vignette, we will use data
from twelve foliage-gleaning bird species collected from point count
surveys at Hubbard Brook Experimental Forest (HBEF) in New Hampshire,
USA. Specific details on the data set, which is just a small subset from
a long-term survey, are available on the Hubbard
Brook website and Doser et al. (2022).
The data are provided as part of the spOccupancy package
and are loaded with data(hbef2015). Point count surveys
were conducted at 373 sites over three replicates, each of 10 minutes in
length and with a detection radius of 100m. In the data set provided
here, we converted these data to detection-nondetection data. Some sites
were not visited for all three replicates. Additional information on the
data set (including individual species in the data set) can be viewed in
the man page using help(hbef2015).
List of 4
$ y : num [1:12, 1:373, 1:3] 0 0 0 0 0 1 0 0 0 0 ...
..- attr(*, "dimnames")=List of 3
.. ..$ : chr [1:12] "AMRE" "BAWW" "BHVI" "BLBW" ...
.. ..$ : chr [1:373] "1" "2" "3" "4" ...
.. ..$ : chr [1:3] "1" "2" "3"
$ occ.covs: num [1:373, 1] 475 494 546 587 588 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : NULL
.. ..$ : chr "Elevation"
$ det.covs:List of 2
..$ day: num [1:373, 1:3] 156 156 156 156 156 156 156 156 156 156 ...
..$ tod: num [1:373, 1:3] 330 346 369 386 409 425 447 463 482 499 ...
$ coords : num [1:373, 1:2] 280000 280000 280000 280001 280000 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:373] "1" "2" "3" "4" ...
.. ..$ : chr [1:2] "X" "Y"Thus, the object hbef2015 is a list comprised of the
detection-nondetection data (y), covariates on the
occurrence portion of the model (occ.covs), covariates on
the detection portion of the model (det.covs), and the
spatial coordinates of each site (coords) for use in
spatial occupancy models and in plotting. This list is in the exact
format required for input to spOccupancy model functions.
hbef2015 contains data on 12 species in the
three-dimensional array y, where the dimensions of
y correspond to species (12), sites (373), and replicates
(3). For single-species occupancy models in Section 2 and 3, we will
only use data on the charming Ovenbird (OVEN; Seiurus
aurocapilla), so we next subset the hbef2015 list to
only include data from OVEN in a new object ovenHBEF.
sp.names <- dimnames(hbef2015$y)[[1]]
ovenHBEF <- hbef2015
ovenHBEF$y <- ovenHBEF$y[sp.names == "OVEN", , ]
table(ovenHBEF$y) # Quick summary.
0 1
518 588 We see that OVEN is detected at a little over half of all site-replicate combinations.
Single-species occupancy models
Basic model description
Let \(z_j\) be the true presence (1) or absence (0) of a species at site \(j\), with \(j = 1, \dots, J\). For our OVEN example, \(J = 373\). Following the basic occupancy model (MacKenzie et al. 2002; Tyre et al. 2003), we assume this latent occurrence variable arises from a Bernoulli process following
\[\begin{equation} \begin{split} &z_j \sim \text{Bernoulli}(\psi_j), \\ &\text{logit}(\psi_j) = \boldsymbol{x}^{\top}_j\boldsymbol{\beta}, \end{split} \end{equation}\]
where \(\psi_j\) is the probability of occurrence at site \(j\), which is a function of site-specific covariates \(\boldsymbol{X}\) and a vector of regression coefficients (\(\boldsymbol{\beta}\)).
We do not directly observe \(z_j\), but rather we observe an imperfect representation of the latent occurrence process as a result of imperfect detection (i.e., the failure to detect a species at a site when it is truly present). Let \(y_{j, k}\) be the observed detection (1) or nondetection (0) of a species of interest at site \(j\) during replicate \(k\) for each of \(k = 1, \dots, K_j\) replicates. Note that the number of replicates, \(K_j\), can vary by site and in practical applications will often be equal to 1 for a subset of sites (i.e., some sites will have no replicate surveys). For our OVEN example, the maximum value of \(K_j\) is three. We envision the detection-nondetection data as arising from a Bernoulli process conditional on the true latent occurrence process:
\[\begin{equation} \begin{split} &y_{j, k} \sim \text{Bernoulli}(p_{j, k}z_j), \\ &\text{logit}(p_{j, k}) = \boldsymbol{v}^{\top}_{j, k}\boldsymbol{\alpha}, \end{split} \end{equation}\]
where \(p_{j, k}\) is the probability of detecting a species at site \(j\) during replicate \(k\) (given it is present at site \(j\)), which is a function of site and replicate specific covariates \(\boldsymbol{V}\) and a vector of regression coefficients (\(\boldsymbol{\alpha}\)).
To complete the Bayesian specification of the model, we assign multivariate normal priors for the occurrence (\(\boldsymbol{\beta}\)) and detection (\(\boldsymbol{\alpha}\)) regression coefficients. To yield an efficient implementation of the occupancy model using a logit link function, we use Pólya-Gamma data augmentation (Polson, Scott, and Windle 2013), which is described in depth in a separate MCMC sampler vignette.
Fitting single-species occupancy models with
PGOcc()
The PGOcc() function fits single-species occupancy
models using Pólya-Gamma latent variables, which makes it more efficient
than standard Bayesian implementations of occupancy models using a logit
link function (Polson, Scott, and Windle 2013;
Clark and Altwegg 2019). PGOcc() has the following
arguments:
PGOcc(occ.formula, det.formula, data, inits, priors, n.samples,
n.omp.threads = 1, verbose = TRUE, n.report = 100,
n.burn = round(.10 * n.samples), n.thin = 1, n.chains = 1,
k.fold, k.fold.threads = 1, k.fold.seed, k.fold.only = FALSE, ...)The first two arguments, occ.formula and
det.formula, use standard R model syntax to denote the
covariates to be included in the occurrence and detection portions of
the model, respectively. Only the right hand side of the formulas are
included. Random intercepts can be included in both the occurrence and
detection portions of the single-species occupancy model using
lme4 syntax (Bates et al.
2015). For example, to include a random intercept for different
observers in the detection portion of the model, we would include
(1 | observer) in the det.formula, where
observer indicates the specific observer for each data
point. The names of variables given in the formulas should correspond to
those found in data, which is a list consisting of the
following tags: y (detection-nondetection data),
occ.covs (occurrence covariates), det.covs
(detection covariates). y should be stored as a sites x
replicate matrix, occ.covs as a matrix or data frame with
site-specific covariate values, and det.covs as a list with
each list element corresponding to a covariate to include in the
detection portion of the model. Covariates on detection can vary by site
and/or survey, and so these covariates may be specified as a site by
survey matrix for survey-level covariates or as a one-dimensional vector
for survey level covariates. The ovenHBEF list is already
in the required format. Here we will model OVEN occurrence as a function
of linear and quadratic elevation and will include three observational
covariates (linear and quadratic day of survey, time of day of survey)
on the detection portion of the model. We standardize all covariates by
using the scale() function in our model specification, and
use the I() function to specify quadratic effects:
oven.occ.formula <- ~ scale(Elevation) + I(scale(Elevation)^2)
oven.det.formula <- ~ scale(day) + scale(tod) + I(scale(day)^2)
# Check out the format of ovenHBEF
str(ovenHBEF)List of 4
$ y : num [1:373, 1:3] 1 1 0 1 0 0 1 0 1 1 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:373] "1" "2" "3" "4" ...
.. ..$ : chr [1:3] "1" "2" "3"
$ occ.covs: num [1:373, 1] 475 494 546 587 588 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : NULL
.. ..$ : chr "Elevation"
$ det.covs:List of 2
..$ day: num [1:373, 1:3] 156 156 156 156 156 156 156 156 156 156 ...
..$ tod: num [1:373, 1:3] 330 346 369 386 409 425 447 463 482 499 ...
$ coords : num [1:373, 1:2] 280000 280000 280000 280001 280000 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:373] "1" "2" "3" "4" ...
.. ..$ : chr [1:2] "X" "Y"Next, we specify the initial values for the MCMC sampler in
inits. PGOcc() (and all other
spOccupancy model fitting functions) will set initial
values by default, but here we will do this explicitly, since in more
complicated cases setting initial values close to the presumed solutions
can be vital for success of an MCMC-based analysis. For all models
described in this vignette (in particular the non-spatial models),
choice of the initial values is largely inconsequential, with the
exception being that specifying initial values close to the presumed
solutions can decrease the amount of samples you need to run to arrive
at convergence of the MCMC chains. Thus, when first running a model in
spOccupancy, we recommend fitting the model using the
default initial values that spOccupancy provides, which are
based on the prior distributions. After running the model for a
reasonable period, if you find the chains are taking a long time to
reach convergence, you then may wish to set the initial values to the
mean estimates of the parameters from the initial model fit, as this
will likely help reduce the amount of time you need to run the
model.
The default initial values for occurrence and detection regression
coefficients (including the intercepts) are random values from the prior
distributions adopted in the model, while the default initial values for
the latent occurrence effects are set to 1 if the species was observed
at a site and 0 otherwise. Initial values are specified in a list with
the following tags: z (latent occurrence values),
alpha (detection intercept and regression coefficients),
and beta (occurrence intercept and regression
coefficients). Below we set all initial values of the regression
coefficients to 0, and set initial values for z based on
the detection-nondetection data matrix. For the occurrence
(beta) and detection (alpha) regression
coefficients, the initial values are passed either as a vector of length
equal to the number of estimated parameters (including an intercept, and
in the order specified in the model formula), or as a single value if
setting the same initial value for all parameters (including the
intercept). Below we take the latter approach. To specify the initial
values for the latent occurrence at each site (z), we must
ensure we set the value to 1 at all sites where OVEN was detected at
least once, because if we detect OVEN at a site then the value of
z is 1 with complete certainty (under the assumption of the
model that there are no false positives). If the initial value for
z is set to 0 at one or more sites when the species was
detected, the occupancy model will fail. spOccupancy will
provide a clear error message if the supplied initial values for
z are invalid. Below we use the raw detection-nondetection
data and the apply() function to set the initial values to
1 if OVEN was detected at that site and 0 otherwise.
# Format with explicit specification of inits for alpha and beta
# with four detection parameters and three occurrence parameters
# (including the intercept).
oven.inits <- list(alpha = c(0, 0, 0, 0),
beta = c(0, 0, 0),
z = apply(ovenHBEF$y, 1, max, na.rm = TRUE))
# Format with abbreviated specification of inits for alpha and beta.
oven.inits <- list(alpha = 0,
beta = 0,
z = apply(ovenHBEF$y, 1, max, na.rm = TRUE))We next specify the priors for the occurrence and detection
regression coefficients. The Pólya-Gamma data augmentation algorithm
employed by spOccupancy assumes normal priors for both the
detection and occurrence regression coefficients. These priors are
specified in a list with tags beta.normal for occurrence
and alpha.normal for detection parameters (including
intercepts). Each list element is then itself a list, with the first
element of the list consisting of the hypermeans for each coefficient
and the second element of the list consisting of the hypervariances for
each coefficient. Alternatively, the hypermean and hypervariances can be
specified as a single value if the same prior is used for all regression
coefficients. By default, spOccupancy will set the
hypermeans to 0 and the hypervariances to 2.72, which corresponds to a
relatively flat prior on the probability scale (0, 1; Lunn et al. (2013)). Broms, Hooten, and Fitzpatrick (2016), Northrup and Gerber (2018), and others show such
priors are an adequate choice when the goal is to specify relatively
non-informative priors. We will use these default priors here, but we
specify them explicitly below for clarity
oven.priors <- list(alpha.normal = list(mean = 0, var = 2.72),
beta.normal = list(mean = 0, var = 2.72))Our last step is to specify the number of samples to produce with the
MCMC algorithm (n.samples), the length of burn-in
(n.burn), the rate at which we want to thin the posterior
samples (n.thin), and the number of MCMC chains to run
(n.chains). Note that currently spOccupancy
runs multiple chains sequentially and does not allow chains to be run
simultaneously in parallel across multiple threads. Instead, we allow
for within-chain parallelization using the n.omp.threads
argument. We can set n.omp.threads to a number greater than
1 and smaller than the number of threads on the computer you are using.
Generally, setting n.omp.threads > 1 will not result in
decreased run times for non-spatial models in spOccupancy,
but can substantially decrease run time when fitting spatial models
(Finley, Datta, and Banerjee 2020). Here
we set n.omp.threads = 1.
For a simple single-species occupancy model, we shouldn’t need too many samples and will only need a small amount of burn-in and thinning. We will run the model using three chains to assess convergence using the Gelman-Rubin diagnostic (Rhat; Brooks and Gelman (1998)).
n.samples <- 5000
n.burn <- 3000
n.thin <- 2
n.chains <- 3We are now nearly set to run the occupancy model. The
verbose argument is a logical value indicating whether or
not MCMC sampler progress is reported to the screen. If
verbose = TRUE, sampler progress is reported after every
multiple of the specified number of iterations in the
n.report argument. We set verbose = TRUE and
n.report = 1000 to report progress after every 1000th MCMC
iteration. The last four arguments to PGOcc()
(k.fold, k.fold.threads,
k.fold.seed, k.fold.only) are used for
performing k-fold cross-validation for model assessment, which we will
illustrate in a subsequent section. For now, we won’t specify the
arguments, which will tell PGOcc() not to perform k-fold
cross-validation.
out <- PGOcc(occ.formula = oven.occ.formula,
det.formula = oven.det.formula,
data = ovenHBEF,
inits = oven.inits,
n.samples = n.samples,
priors = oven.priors,
n.omp.threads = 1,
verbose = TRUE,
n.report = 1000,
n.burn = n.burn,
n.thin = n.thin,
n.chains = n.chains)----------------------------------------
Preparing to run the model
----------------------------------------
----------------------------------------
Model description
----------------------------------------
Occupancy model with Polya-Gamma latent
variable fit with 373 sites.
Samples per Chain: 5000
Burn-in: 3000
Thinning Rate: 2
Number of Chains: 3
Total Posterior Samples: 3000
Source compiled with OpenMP support and model fit using 1 thread(s).
----------------------------------------
Chain 1
----------------------------------------
Sampling ...
Sampled: 1000 of 5000, 20.00%
-------------------------------------------------
Sampled: 2000 of 5000, 40.00%
-------------------------------------------------
Sampled: 3000 of 5000, 60.00%
-------------------------------------------------
Sampled: 4000 of 5000, 80.00%
-------------------------------------------------
Sampled: 5000 of 5000, 100.00%
----------------------------------------
Chain 2
----------------------------------------
Sampling ...
Sampled: 1000 of 5000, 20.00%
-------------------------------------------------
Sampled: 2000 of 5000, 40.00%
-------------------------------------------------
Sampled: 3000 of 5000, 60.00%
-------------------------------------------------
Sampled: 4000 of 5000, 80.00%
-------------------------------------------------
Sampled: 5000 of 5000, 100.00%
----------------------------------------
Chain 3
----------------------------------------
Sampling ...
Sampled: 1000 of 5000, 20.00%
-------------------------------------------------
Sampled: 2000 of 5000, 40.00%
-------------------------------------------------
Sampled: 3000 of 5000, 60.00%
-------------------------------------------------
Sampled: 4000 of 5000, 80.00%
-------------------------------------------------
Sampled: 5000 of 5000, 100.00%
names(out) # Look at the contents of the resulting object. [1] "rhat" "beta.samples" "alpha.samples" "z.samples"
[5] "psi.samples" "like.samples" "ESS" "X"
[9] "X.p" "X.re" "X.p.re" "y"
[13] "n.samples" "call" "n.post" "n.thin"
[17] "n.burn" "n.chains" "pRE" "psiRE"
[21] "run.time" PGOcc() returns a list of class PGOcc with
a suite of different objects, many of them being coda::mcmc
objects of posterior samples. Note the “Preparing to run the model”
printed section doesn’t have any information shown in it.
spOccupancy model fitting functions will present messages
when preparing the data for the model in this section, or will print out
the default priors or initial values used when they are not specified in
the function call. Here we specified everything explicitly so no
information was reported.
For a concise yet informative summary of the regression parameters
and convergence of the MCMC chains, we can use summary() on
the resulting PGOcc() object.
summary(out)
Call:
PGOcc(occ.formula = oven.occ.formula, det.formula = oven.det.formula,
data = ovenHBEF, inits = oven.inits, priors = oven.priors,
n.samples = n.samples, n.omp.threads = 1, verbose = TRUE,
n.report = 1000, n.burn = n.burn, n.thin = n.thin, n.chains = n.chains)
Samples per Chain: 5000
Burn-in: 3000
Thinning Rate: 2
Number of Chains: 3
Total Posterior Samples: 3000
Run Time (min): 0.073
Occurrence (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) 2.1370 0.2728 1.6490 2.1188 2.7079 1.0001 834
scale(Elevation) -1.7024 0.2983 -2.4095 -1.6701 -1.2336 1.0100 402
I(scale(Elevation)^2) -0.3992 0.2038 -0.7687 -0.4103 0.0481 1.0030 645
Detection (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) 0.7942 0.1269 0.5394 0.7940 1.0407 1.0018 2694
scale(day) -0.0904 0.0773 -0.2450 -0.0910 0.0587 1.0021 3814
scale(tod) -0.0460 0.0781 -0.2008 -0.0457 0.1030 0.9996 3000
I(scale(day)^2) 0.0238 0.0966 -0.1625 0.0231 0.2209 1.0053 3000Note that all coefficients are printed on the logit scale. We see
OVEN is fairly widespread (at the scale of the survey) in the forest
given the large intercept value, which translates to a value of 0.89 on
the probability scale (run plogis(2.13)). In addition, the
negative linear and quadratic terms for Elevation suggest
occurrence probability peaks at mid-elevations. On average, detection
probability is about 0.69.
In principle, before we even look at the parameter summaries, we
ought to ensure that the MCMC chains have reached convergence. The
summary function also returns the Gelman-Rubin diagnostic
(Brooks and Gelman 1998) and the effective
samples size (ESS) of the posterior samples, which we can use to assess
convergence. Here we see all Rhat values are less than 1.1 and the ESS
values indicate adequate mixing of the MCMC chains. Additionally, we can
use the plot() function to plot traceplots of the
individual model parameters that are contained in the resulting
PGOcc object. The plot() function takes three
arguments: x (the model object), param (a
character string denoting the parameter name), and density
(logical value indicating whether to also plot the density of MCMC
samples along with the traceplot). See ?plot.PGOcc for more
details (similar functions exist for all spOccupancy model
objects).
plot(out, 'beta', density = FALSE) # Occupancy parameters.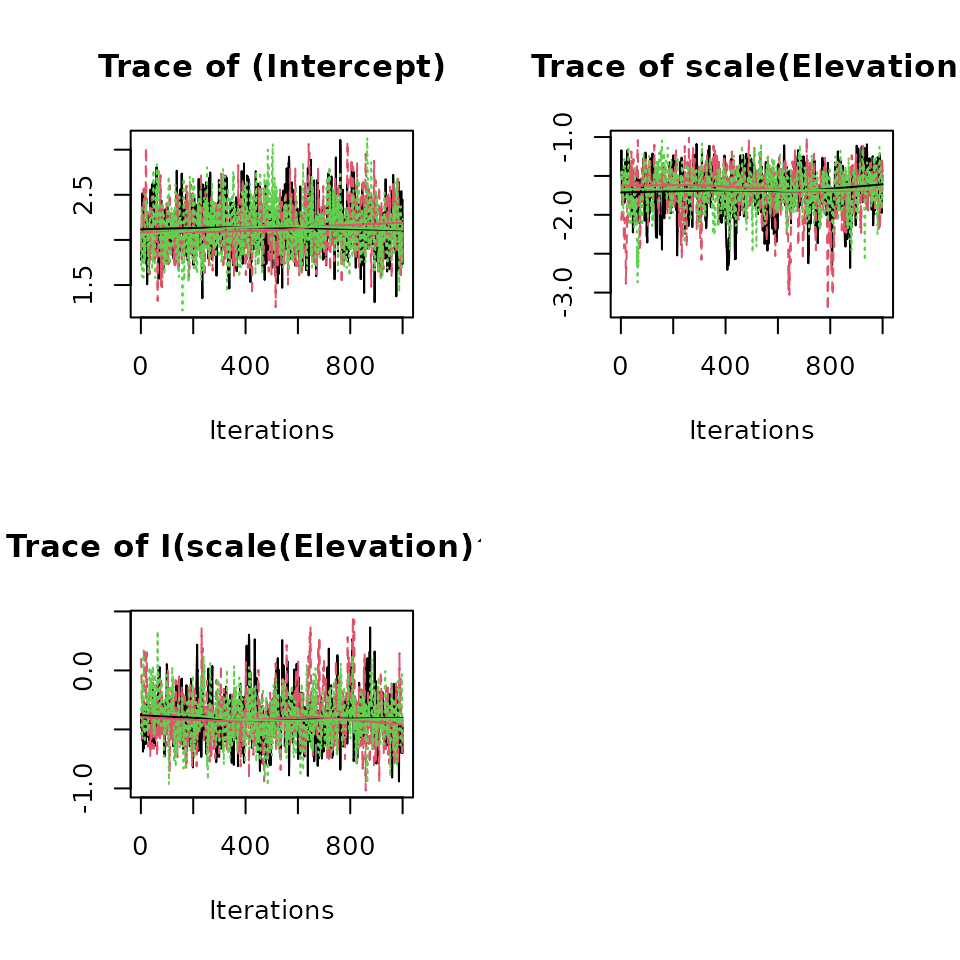
plot(out, 'alpha', density = FALSE) # Detection parameters.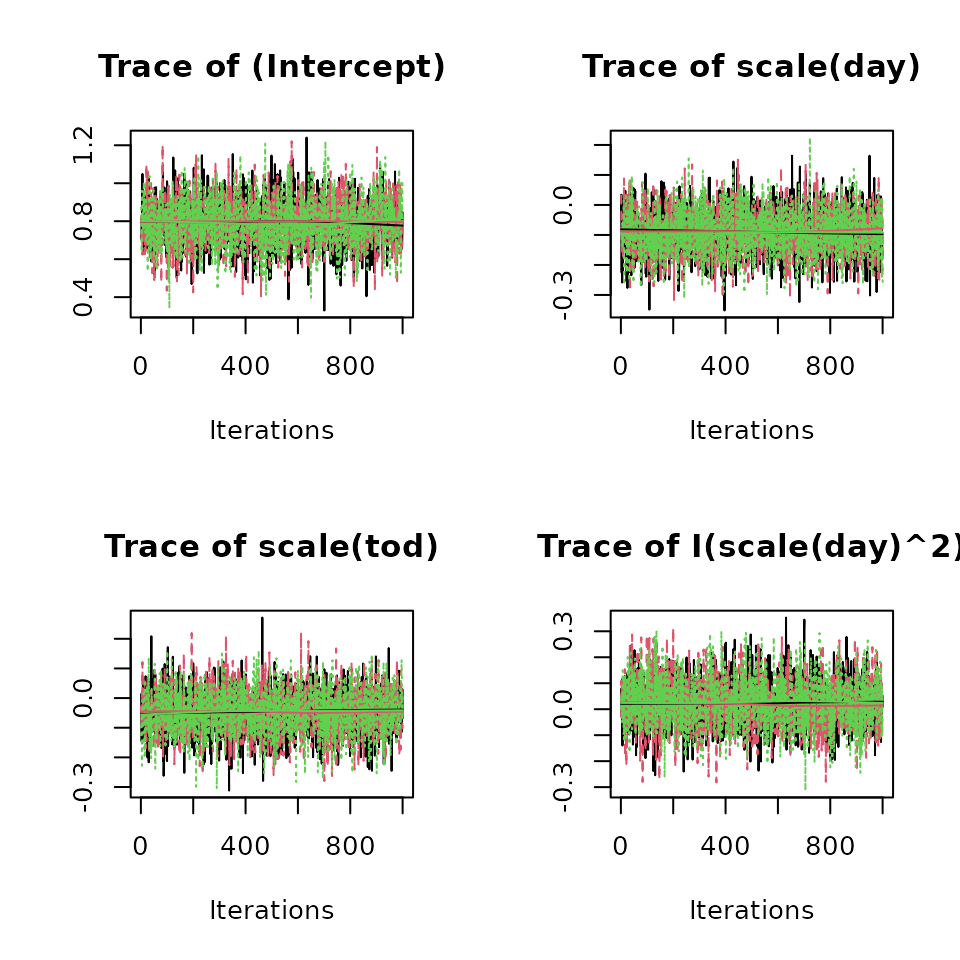
Posterior predictive checks
The function ppcOcc() performs a posterior predictive
check on all spOccupancy model objects as a Goodness of Fit
(GoF) assessment. The fundamental idea of GoF testing is that a good
model should generate data that closely align with the observed data. If
there are drastic differences in the true data from the model generated
data, our model is likely not very useful (Hobbs
and Hooten 2015). GoF assessments are more complicated using
binary data, like detection-nondetection used in occupancy models, as
standard approaches are not valid assessments for the raw data in binary
response models such as occupancy models (Broms,
Hooten, and Fitzpatrick 2016; McCullagh and Nelder 2019). Thus,
any approach to assess model fit for detection-nondetection data must
bin, or aggregate, the raw values in some manner, and then perform a
model fit assessment on the binned values. There are numerous ways we
could envision binning the raw detection-nondetection values (MacKenzie and Bailey 2004; Kéry and Royle
2016). In spOccupancy, a posterior predictive check
broadly takes the following steps:
- Fit the model using any of the model-fitting functions (here
PGOcc()), which generates replicated values for all detection-nondetection data points. - Bin both the actual and the replicated detection-nondetection data in a suitable manner, such as by site or replicate (MacKenzie and Bailey 2004).
- Compute a fit statistic on both the actual data and also on the model-generated ‘replicate data’.
- Compare the fit statistics for the true data and replicate data. If they are widely different, this suggests a lack of fit of the model to the actual data set at hand.
To perform a posterior predictive check, we send the resulting
PGOcc model object as input to the ppcOcc()
function, along with a fit statistic (fit.stat) and a
numeric value indicating how to group, or bin, the data
(group). Currently supported fit statistics include the
Freeman-Tukey statistic and the Chi-Squared statistic
(freeman-tukey or chi-squared, respectively,
Kéry and Royle (2016)). Currently,
ppcOcc() allows the user to group the data by row (site;
group = 1) or column (replicate; group = 2).
ppcOcc() will then return a set of posterior samples for
the fit statistic (or discrepancy measure) using the actual data
(fit.y) and model generated replicate data set
(fit.y.rep), summed across all data points in the chosen
manner. We generally recommend performing a posterior predictive check
when grouping data both across sites (group = 1) as well as
across replicates (group = 2), as they may reveal (or fail
to reveal) different inadequacies of the model for the specific data set
at hand (Kéry and Royle 2016). In
particular, binning the data across sites (group = 1) may
help reveal whether the model fails to adequately represent variation in
occurrence and detection probability across space, while binning the
data across replicates (group = 2) may help reveal whether
the model fails to adequately represent variation in detection
probability across the different replicate surveys. Similarly, we
suggest exploring posterior predictive checks using both the
Freeman-Tukey Statistic as well as the Chi-Squared statistic. Generally,
the more ways we explore the fit of our model to the data, the more
confidence we have that our model is adequately representing the data
and we can draw reasonable conclusions from it. By performing posterior
predictive checks with the two fit statistics and two ways of grouping
the data, spOccupancy provides us with four different
measures that we can use to assess the validity of our model. Throughout
this vignette, we will display different types of posterior predictive
checks using different combinations of the fit statistic and grouping
approach. In a more complete analysis, we would run all four types of
posterior predictive checks for each model we fit as a more complete GoF
assessment.
The resulting values from a call to ppcOcc() can be used
with the summary() function to generate a Bayesian p-value,
which is the probability, under the fitted model, to obtain a value of
the fit statistic that is more extreme (i.e., larger) than the one
observed, i.e., for the actual data. Bayesian p-values are sensitive to
individual values, so we should also explore the discrepancy measures
for each “grouped” data point. ppcOcc() returns a matrix of
posterior quantiles for the fit statistic for both the observed
(fit.y.group.quants) and model generated, replicate data
(fit.y.rep.group.quants) for each “grouped” data point.
We next perform a posterior predictive check using the Freeman-Tukey
statistic grouping the data by sites. We summarize the posterior
predictive check with the summary() function, which reports
a Bayesian p-value. A Bayesian p-value that hovers around 0.5 indicates
adequate model fit, while values less than 0.1 or greater than 0.9
suggest our model does not fit the data well (Hobbs and Hooten 2015). As always with a
simulation-based analysis using MCMC, you will get numerically slightly
different values.
Call:
ppcOcc(object = out, fit.stat = "freeman-tukey", group = 1)
Samples per Chain: 5000
Burn-in: 3000
Thinning Rate: 2
Number of Chains: 3
Total Posterior Samples: 3000
Bayesian p-value: 0.2403
Fit statistic: freeman-tukey The Bayesian p-value is the proportion of posterior samples of the fit statistic of the model generated data that are greater than the corresponding fit statistic of the true data, summed across all “grouped” data points. We can create a visual representation of the Bayesian p-value as follows (Kéry and Royle 2016):
ppc.df <- data.frame(fit = ppc.out$fit.y,
fit.rep = ppc.out$fit.y.rep,
color = 'lightskyblue1')
ppc.df$color[ppc.df$fit.rep > ppc.df$fit] <- 'lightsalmon'
plot(ppc.df$fit, ppc.df$fit.rep, bg = ppc.df$color, pch = 21,
ylab = 'Fit', xlab = 'True')
lines(ppc.df$fit, ppc.df$fit, col = 'black')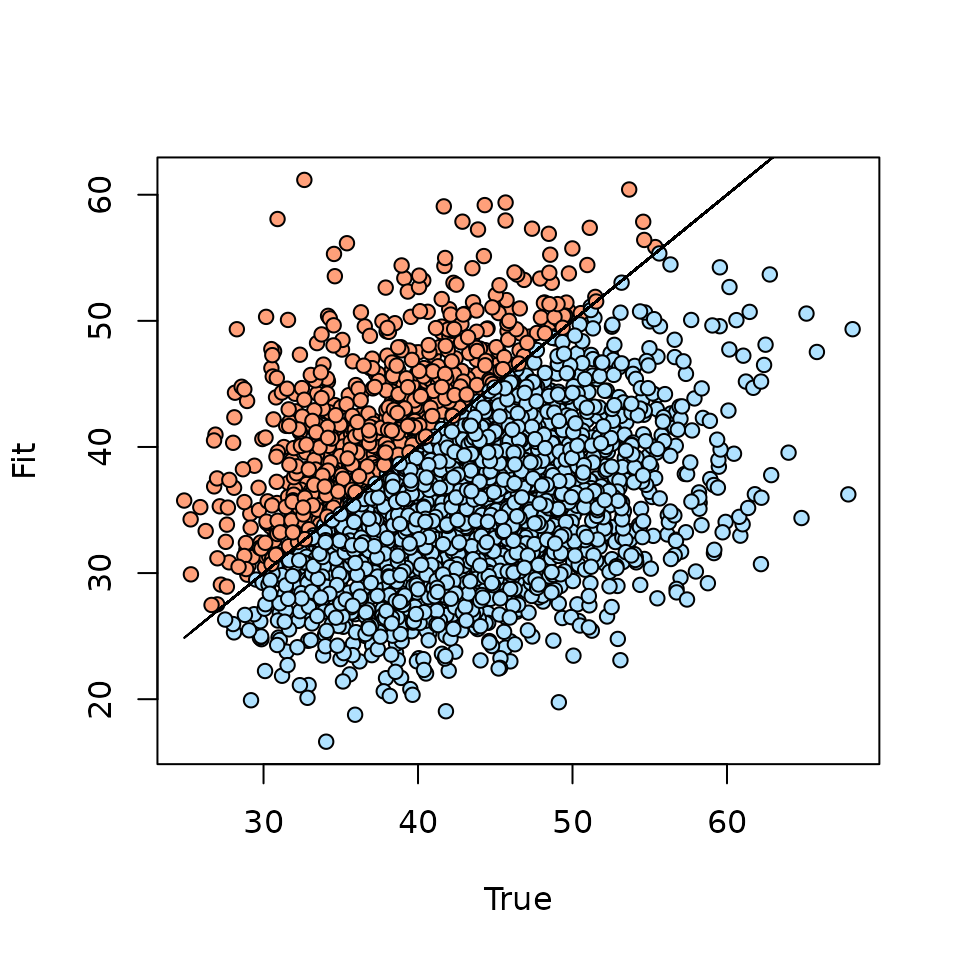
Our Bayesian p-value is greater than 0.1 indicating no lack of fit,
although the above plot shows most of the fit statistics are smaller for
the replicate data than the actual data set. Relying solely on the
Bayesian p-value as an assessment of model fit is not always a great
option, as individual data points can have an overbearing influence on
the resulting summary value. Instead of summing across all data points
for a single discrepancy measure, ppcOcc() also allows us
to explore discrepancy measures on a “grouped” point by point basis. The
resulting ppcOcc object will contain the objects
fit.y.group.quants and fit.y.rep.group.quants,
which contain quantiles of the posterior distributions for the
discrepancy measures of each grouped data point. Below we plot the
difference in the discrepancy measure between the replicate and actual
data across each of the sites.
diff.fit <- ppc.out$fit.y.rep.group.quants[3, ] - ppc.out$fit.y.group.quants[3, ]
plot(diff.fit, pch = 19, xlab = 'Site ID', ylab = 'Replicate - True Discrepancy')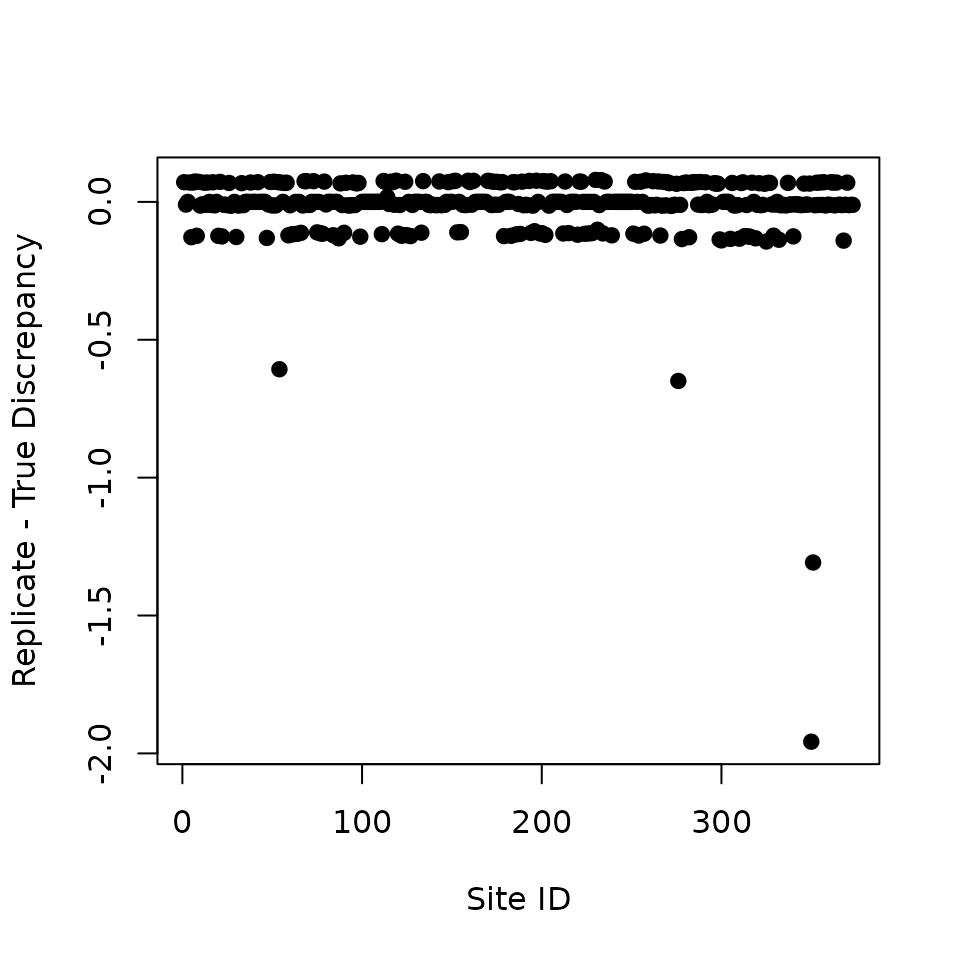
We see there are four sites that contribute to the overall GoF measure far more than in proportion to their number, i.e., whose discrepancy measure for the actual data is much larger than the corresponding discrepancy for the replicate data. Here we will ignore this, but in a real analysis it might be very insightful to further explore these sites to see what could explain this pattern (e.g., are the sites close together in space? Could the data be the result of erroneous recording, or of extraordinary local habitat that is not adequately described by the occurrence covariates?). Although rarely done, closer investigations of outlying values in statistical analyses may sometimes teach one more than mere acceptance of a fitting model.
Model selection using WAIC and k-fold cross-validation
Posterior predictive checks allow us to assess how well our model fits the data, but they are not very useful if we want to compare multiple competing models and ultimately select a final model based on some criterion. Bayesian model selection is very much a constantly changing field. See Hooten and Hobbs (2015) for an accessible overview of Bayesian model selection for ecologists.
For Bayesian hierarchical models like occupancy models, the most common Bayesian model selection criterion, the deviance information criterion or DIC, is not applicable (Hooten and Hobbs 2015). Instead, the Widely Applicable Information Criterion (Watanabe 2010) is recommended to compare a set of models and select the best-performing model for final analysis.
The WAIC is calculated for all spOccupancy model objects
using the function waicOcc(). We calculate the WAIC as
\[ \text{WAIC} = -2 \times (\text{elpd} - \text{pD}), \]
where elpd is the expected log point-wise predictive density and PD is the effective number of parameters. We calculate elpd by calculating the likelihood for each posterior sample, taking the mean of these likelihood values, taking the log of the mean of the likelihood values, and summing these values across all sites. We calculate the effective number of parameters by calculating the variance of the log likelihood for each site taken over all posterior samples, and then summing these values across all sites. See Appendix S1 from Broms, Hooten, and Fitzpatrick (2016) for more details.
We calculate the WAIC using waicOcc() for our OVEN model
below (as always, note some slight differences with your solutions due
to Monte Carlo error).
waicOcc(out) elpd pD WAIC
-632.960543 6.290149 1278.501382 For illustration, let’s next rerun the OVEN model, but this time we assume occurrence is constant across the HBEF, and subsequently compare the WAIC value to the full model
out.small <- PGOcc(occ.formula = ~ 1,
det.formula = oven.det.formula,
data = ovenHBEF,
inits = oven.inits,
n.samples = n.samples,
priors = oven.priors,
n.omp.threads = 1,
verbose = FALSE,
n.burn = n.burn,
n.thin = n.thin,
n.chains = n.chains)
waicOcc(out.small) elpd pD WAIC
-692.046183 4.932945 1393.958257 Smaller values of WAIC indicate models with better performance. We see the WAIC for the model with elevation is smaller than the intercept-only model, indicating elevation is an important predictor for OVEN occurrence in HBEF.
When focusing primarily on predictive performance, a k-fold
cross-validation (CV) approach is another attractive, though
computationally more intensive, alternative to compare a series of
models, especially since WAIC may not always be reliable for occupancy
models (Broms, Hooten, and Fitzpatrick
2016). In spOccupancy, k-fold cross-validation is
accomplished using the arguments k.fold,
k.fold.threads, and k.fold.seed in the model
fitting function. A k-fold cross validation approach requires fitting a
model \(k\) times, where each time the
model is fit using \(J / k\) data
points, where \(J\) is the total number
of sites surveyed at least once in the data set. Each time the model is
fit, it uses a different portion of the data and then predicts the
remaining \(J - J/k\) hold out values.
Because the data are not used to fit the model, CV yields true samples
from the posterior predictive distribution that we can use to assess the
predictive capacity of the model.
As a measure of out-of-sample predictive performance, we use the deviance as a scoring rule following Hooten and Hobbs (2015). For K-fold cross-validation, it is computed as
\[\begin{equation} -2 \sum_{k = 1}^K \text{log}\Bigg(\frac{\sum_{q = 1}^Q \text{Bernoulli}(\boldsymbol{y}_k \mid \boldsymbol{p}^{(q)}\boldsymbol{z}_k^{(q)})}{Q}\Bigg), \end{equation}\]
where \(\boldsymbol{p}^{(q)}\) and
\(\boldsymbol{z}_k^{(q)}\) are MCMC
samples of detection probability and latent occurrence, respectively,
arising from a model that is fit without the observations \(\boldsymbol{y}_k\), and \(Q\) is the total number of posterior
samples produced from the MCMC sampler. The -2 is used so that smaller
values indicate better model fit, which aligns with most information
criteria used for model assessment (like the WAIC implemented using
waicOcc()).
The three arguments in PGOcc() (k.fold,
k.fold.threads, k.fold.seed) control whether
or not k-fold cross validation is performed following the complete fit
of the model using the entire data set. The k.fold argument
indicates the number of \(k\) folds to
use for cross-validation. If k.fold is not specified,
cross-validation is not performed and k.fold.threads and
k.fold.seed are ignored. The k.fold.threads
argument indicates the number of threads to use for running the \(k\) models in parallel across multiple
threads. Parallel processing is accomplished using the R packages
foreach and doParallel. Specifying
k.fold.threads > 1 can substantially decrease run time
since it allows for models to be fit simultaneously on different threads
rather than sequentially. The k.fold.seed indicates the
seed used to randomly split the data into \(k\) groups. This is by default set to 100.
Lastly, the k.fold.only argument controls whether the full
model is run prior to performing cross-validation
(k.fold.only = FALSE, the default). If set to
TRUE, only k-fold cross-validation will be performed. This
can be useful when performing cross-validation after doing some initial
exploration with fitting different models with the full data set so that
you don’t have to rerun the full model again.
Below we refit the occupancy model with elevation (linear and
quadratic) as an occurrence predictor this time performing 4-fold
cross-validation. We set k.fold = 4 to perform 4-fold
cross-validation and k.fold.threads = 1 to run the model
using 1 thread. Normally we would set k.fold.threads = 4,
but using multiple threads leads to complications when compiling this
vignette, so we leave that to you to explore the computational
improvements of performing cross-validation across multiple cores.
out.k.fold <- PGOcc(occ.formula = oven.occ.formula,
det.formula = oven.det.formula,
data = ovenHBEF,
inits = oven.inits,
n.samples = n.samples,
priors = oven.priors,
n.omp.threads = 1,
verbose = TRUE,
n.report = 1000,
n.burn = n.burn,
n.thin = n.thin,
n.chains = n.chains,
k.fold = 4,
k.fold.threads = 1)----------------------------------------
Preparing to run the model
----------------------------------------
----------------------------------------
Model description
----------------------------------------
Occupancy model with Polya-Gamma latent
variable fit with 373 sites.
Samples per Chain: 5000
Burn-in: 3000
Thinning Rate: 2
Number of Chains: 3
Total Posterior Samples: 3000
Source compiled with OpenMP support and model fit using 1 thread(s).
----------------------------------------
Chain 1
----------------------------------------
Sampling ...
Sampled: 1000 of 5000, 20.00%
-------------------------------------------------
Sampled: 2000 of 5000, 40.00%
-------------------------------------------------
Sampled: 3000 of 5000, 60.00%
-------------------------------------------------
Sampled: 4000 of 5000, 80.00%
-------------------------------------------------
Sampled: 5000 of 5000, 100.00%
----------------------------------------
Chain 2
----------------------------------------
Sampling ...
Sampled: 1000 of 5000, 20.00%
-------------------------------------------------
Sampled: 2000 of 5000, 40.00%
-------------------------------------------------
Sampled: 3000 of 5000, 60.00%
-------------------------------------------------
Sampled: 4000 of 5000, 80.00%
-------------------------------------------------
Sampled: 5000 of 5000, 100.00%
----------------------------------------
Chain 3
----------------------------------------
Sampling ...
Sampled: 1000 of 5000, 20.00%
-------------------------------------------------
Sampled: 2000 of 5000, 40.00%
-------------------------------------------------
Sampled: 3000 of 5000, 60.00%
-------------------------------------------------
Sampled: 4000 of 5000, 80.00%
-------------------------------------------------
Sampled: 5000 of 5000, 100.00%
----------------------------------------
Cross-validation
----------------------------------------Performing 4-fold cross-validation using 1 thread(s).We subsequently refit the intercept only occupancy model, and compare the deviance metrics from the 4-fold cross-validation.
# Model fitting information is suppressed for space.
out.int.k.fold <- PGOcc(occ.formula = ~ 1,
det.formula = oven.det.formula,
data = ovenHBEF,
inits = oven.inits,
n.samples = n.samples,
priors = oven.priors,
n.omp.threads = 1,
verbose = FALSE,
n.report = 1000,
n.burn = n.burn,
n.thin = n.thin,
n.chains = n.chains,
k.fold = 4,
k.fold.threads = 1)The cross-validation metric (model deviance) is stored in the
k.fold.deviance tag of the resulting model object.
out.k.fold$k.fold.deviance # Larger model. [1] 1332.179
out.int.k.fold$k.fold.deviance # Intercept-only model.[1] 1533.212Similar to the results from the WAIC, CV also suggests that the model including elevation with a predictor outperforms the intercept only model.
Prediction
All model objects resulting from a call to spOccupancy
model-fitting functions can be used with predict() to
generate a series of posterior predictive samples at new locations,
given the values of all covariates used in the model fitting process.
The object hbefElev (which comes as part of the
spOccupancy package) contains elevation data at a 30x30m
resolution from the National Elevation Data set across the entire HBEF.
We load the data below
'data.frame': 46090 obs. of 3 variables:
$ val : num 914 916 918 920 922 ...
$ Easting : num 276273 276296 276318 276340 276363 ...
$ Northing: num 4871424 4871424 4871424 4871424 4871424 ...The column val contains the elevation values, while
Easting and Northing contain the spatial
coordinates that we will use for plotting. We can obtain posterior
predictive samples for the occurrence probabilities at these sites by
using the predict() function and our PGOcc
fitted model object. Given that we standardized the elevation values
when we fit the model, we need to standardize the elevation values for
prediction using the exact same values of the mean and standard
deviation of the elevation values used to fit the data.
elev.pred <- (hbefElev$val - mean(ovenHBEF$occ.covs[, 1])) / sd(ovenHBEF$occ.covs[, 1])
# These are the new intercept and covariate data.
X.0 <- cbind(1, elev.pred, elev.pred^2)
out.pred <- predict(out, X.0)For PGOcc objects, the predict function
takes two arguments: (1) the PGOcc fitted model object; and
(2) a matrix or data frame consisting of the design matrix for the
prediction locations (which must include and intercept if our model
contained one). The resulting object consists of posterior predictive
samples for the latent occurrence probabilities
(psi.0.samples) and latent occurrence values
(z.0.samples). The beauty of the Bayesian paradigm, and the
MCMC computing machinery, is that these predictions all have fully
propagated uncertainty. We can use these values to create plots of the
predicted mean occurrence values, as well as of their standard deviation
as a measure of the uncertainty in these predictions akin to a standard
error associated with maximum likelihood estimates. We could also
produce a map for the Bayesian credible interval length as an
alternative measure of prediction uncertainty or two maps, one showing
the lower and the other the upper limit of, say, a 95% credible
interval.
plot.dat <- data.frame(x = hbefElev$Easting,
y = hbefElev$Northing,
mean.psi = apply(out.pred$psi.0.samples, 2, mean),
sd.psi = apply(out.pred$psi.0.samples, 2, sd),
stringsAsFactors = FALSE)
# Make a species distribution map showing the point estimates,
# or predictions (posterior means)
dat.stars <- st_as_stars(plot.dat, dims = c('x', 'y'))
ggplot() +
geom_stars(data = dat.stars, aes(x = x, y = y, fill = mean.psi)) +
scale_fill_viridis_c(na.value = 'transparent') +
labs(x = 'Easting', y = 'Northing', fill = '',
title = 'Mean OVEN occurrence probability') +
theme_bw()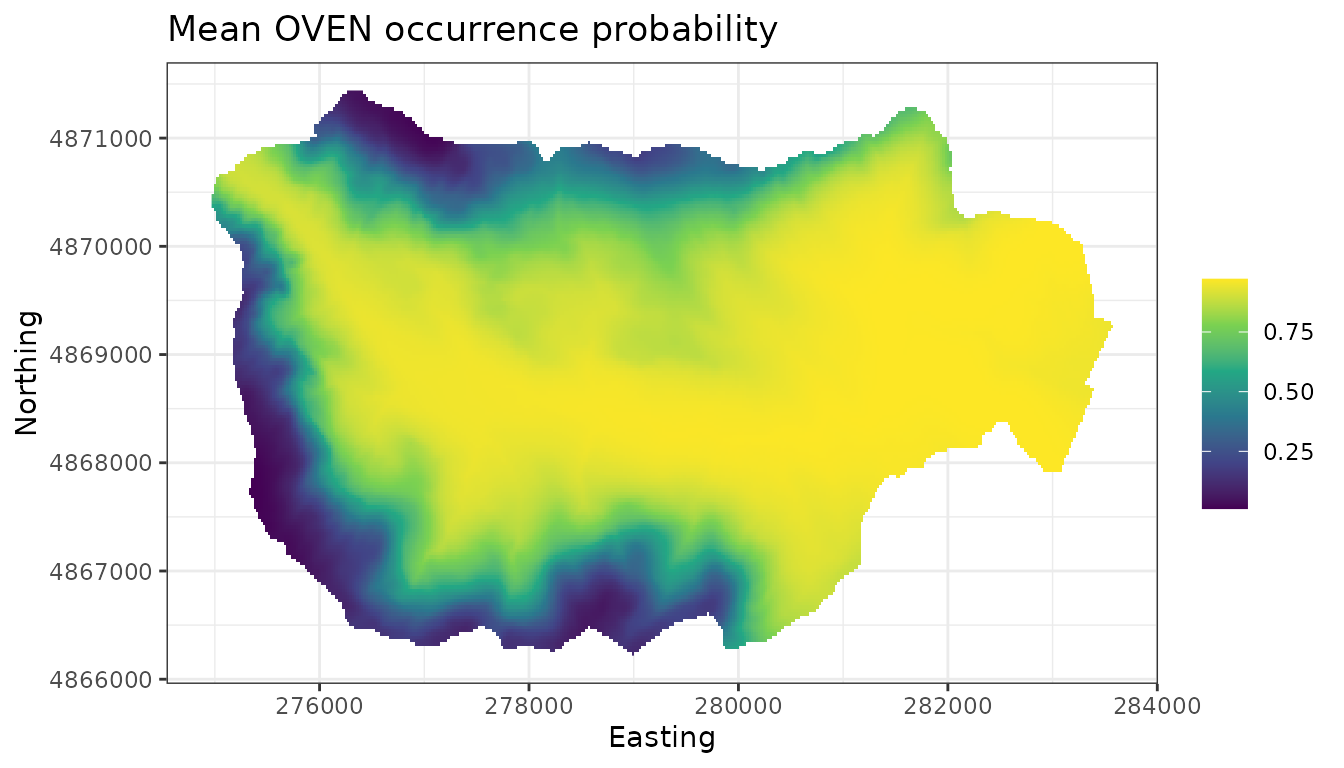
# Map of the associated uncertainty of these predictions
# (i.e., posterior sds)
ggplot() +
geom_stars(data = dat.stars, aes(x = x, y = y, fill = sd.psi)) +
scale_fill_viridis_c(na.value = 'transparent') +
labs(x = 'Easting', y = 'Northing', fill = '',
title = 'SD OVEN occurrence probability') +
theme_bw()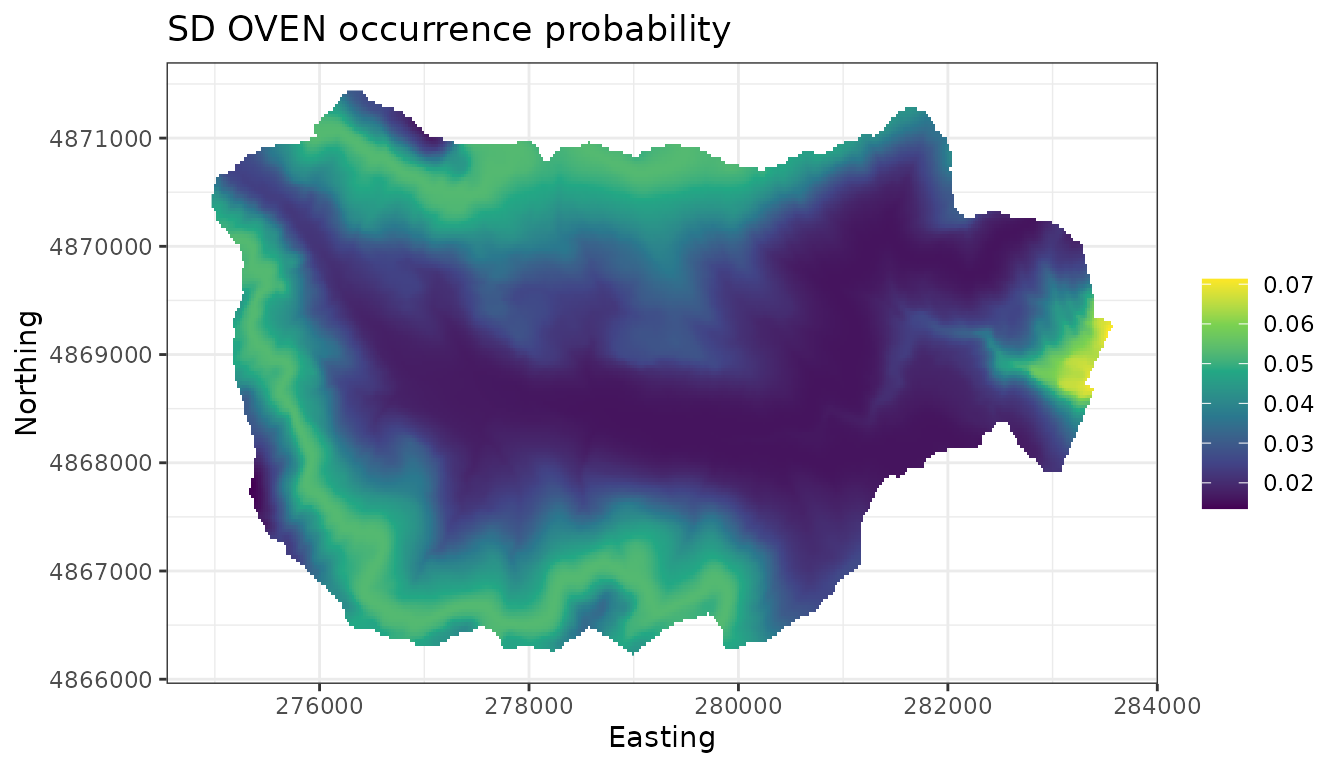
Single-species spatial occupancy models
Basic model description
When working across large spatial domains, accounting for residual spatial autocorrelation in species distributions can often improve predictive performance of a model, leading to more accurate species distribution maps (Guélat and Kéry 2018; Lany et al. 2020). We here extend the basic single-species occupancy model to incorporate a spatial Gaussian Process that accounts for unexplained spatial variation in species occurrence across a region of interest. Let \(\boldsymbol{s}_j\) denote the geographical coordinates of site \(j\) for \(j = 1, \dots, J\). In all spatially-explicit models, we include \(\boldsymbol{s}_j\) directly in the notation of spatially-indexed variables to indicate the model is spatially-explicit. More specifically, the occurrence probability at site \(j\) with coordinates \(\boldsymbol{s}_j\), \(\psi(\boldsymbol{s}_j)\), now takes the form
\[\begin{equation} \text{logit}(\psi(\boldsymbol{s}_j) = \boldsymbol{x}(\boldsymbol{s}_j)^{\top}\boldsymbol{\beta} + \omega(\boldsymbol{s}_j), \end{equation}\]
where \(\omega_j\) is a realization from a zero-mean spatial Gaussian Process, i.e.,
\[\begin{equation} \boldsymbol{\omega}(\boldsymbol{s}) \sim N(\boldsymbol{0}, \boldsymbol{\Sigma}(\boldsymbol{\boldsymbol{s}, \boldsymbol{s}', \theta})). \end{equation}\]
We define \(\boldsymbol{\Sigma}(\boldsymbol{s}, \boldsymbol{s}', \boldsymbol{\theta})\) as a \(J \times J\) covariance matrix that is a function of the distances between any pair of site coordinates \(\boldsymbol{s}\) and \(\boldsymbol{s}'\) and a set of parameters \((\boldsymbol{\theta})\) that govern the spatial process. The vector \(\boldsymbol{\theta}\) is equal to \(\boldsymbol{\theta} = \{\sigma^2, \phi, \nu\}\), where \(\sigma^2\) is a spatial variance parameter, \(\phi\) is a spatial decay parameter, and \(\nu\) is a spatial smoothness parameter. \(\nu\) is only specified when using a Matern correlation function.
The detection portion of the occupancy model remains unchanged from
the non-spatial occupancy model. Single-species spatial occupancy
models, like all models in spOccupancy are fit using
Pólya-Gamma data augmentation (see MCMC sampler vignette for
details).
When the number of sites is moderately large, say 1000, the above described spatial Gaussian process model can become drastically slow as a result of the need to take the inverse of the spatial covariance matrix \(\boldsymbol{\Sigma}(\boldsymbol{s}, \boldsymbol{s}', \boldsymbol{\theta})\) at each MCMC iteration. Numerous approximation methods exist to reduce this computational cost (see Heaton et al. (2019) for an overview and comparison of multiple methods). One attractive approach is the Nearest Neighbor Gaussian Process (NNGP; Datta et al. (2016)). Instead of modeling the spatial process using a full Gaussian Process, we replace the Gaussian Process prior specification with a NNGP, which leads to drastic improvements of run time with nearly identical inference and prediction as the full Gaussian Process specification. See Datta et al. (2016), Finley et al. (2019), and the MCMC sampler vignette for additional statistical details on NNGPs and their implementation in spatial occupancy models.
Fitting single-species spatial occupancy models with
spPGOcc()
The function spPGOcc() fits single-species spatial
occupancy models using Pólya-Gamma latent variables, where spatial
autocorrelation is accounted for using a spatial Gaussian Process.
spPGOcc() fits spatial occupancy models using either a full
Gaussian process or an NNGP. See Finley, Datta,
and Banerjee (2020) for details on using NNGPs with Pólya-Gamma
latent variables.
We will fit the same occupancy model for OVEN that we fit previously
using PGOcc(), but we will now make the model spatially
explicit by incorporating a spatial process with spPGOcc().
First, let’s take a look at the arguments for
spPGOcc():
spPGOcc(occ.formula, det.formula, data, inits, n.batch,
batch.length, accept.rate = 0.43, priors,
cov.model = "exponential", tuning, n.omp.threads = 1,
verbose = TRUE, NNGP = FALSE, n.neighbors = 15,
search.type = "cb", n.report = 100,
n.burn = round(.10 * n.batch * batch.length),
n.thin = 1, n.chains = 1, k.fold, k.fold.threads = 1,
k.fold.seed = 100, k.fold.only = FALSE, ...)We will walk through each of the arguments to spPGOcc()
in the context of our Ovenbird example. The occurrence
(occ.formula) and detection (det.formula)
formulas, as well as the list of data (data), take the same
form as we saw in PGOcc, with random intercepts allowed in
both the occurrence and detection models. Notice the coords
matrix in the ovenHBEF list of data. We did not use this
for PGOcc() but specifying the spatial coordinates in
data is required for all spatially explicit models in
spOccupancy.
oven.occ.formula <- ~ scale(Elevation) + I(scale(Elevation)^2)
oven.det.formula <- ~ scale(day) + scale(tod) + I(scale(day)^2)
str(ovenHBEF) # coords is required for spPGOcc.List of 4
$ y : num [1:373, 1:3] 1 1 0 1 0 0 1 0 1 1 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:373] "1" "2" "3" "4" ...
.. ..$ : chr [1:3] "1" "2" "3"
$ occ.covs: num [1:373, 1] 475 494 546 587 588 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : NULL
.. ..$ : chr "Elevation"
$ det.covs:List of 2
..$ day: num [1:373, 1:3] 156 156 156 156 156 156 156 156 156 156 ...
..$ tod: num [1:373, 1:3] 330 346 369 386 409 425 447 463 482 499 ...
$ coords : num [1:373, 1:2] 280000 280000 280000 280001 280000 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:373] "1" "2" "3" "4" ...
.. ..$ : chr [1:2] "X" "Y"The initial values (inits) are again specified in a
list. Valid tags for initial values now additionally include the
parameters associated with the spatial random effects. These include:
sigma.sq (spatial variance parameter), phi
(spatial range parameter), w (the latent spatial random
effects at each site), and nu (spatial smoothness
parameter), where the latter is only specified if adopting a Matern
covariance function (i.e., cov.model = 'matern').
spOccupancy supports four spatial covariance models
(exponential, spherical,
gaussian, and matern), which are specified in
the cov.model argument. Throughout this vignette, we will
use an exponential covariance model, which we often use as our default
covariance model when fitting spatially-explicit models and is commonly
used throughout ecology. To determine which covariance function to use,
we can fit models with the different covariance functions and compare
them using WAIC or k-fold cross-validation to select the best performing
function. We will note that the Matern covariance function has the
additional spatial smoothness parameter \(\nu\) and thus can often be more flexible
than the other functions. However, because we need to estimate an
additional parameter, this also tends to require more data (i.e., a
larger number of sites) than the other covariance functions, and so we
encourage use of the three simpler functions if your data set is sparse.
We note that model estimates are generally fairly robust to the
different covariance functions, although certain functions may provide
substantially better estimates depending on the specific form of the
underlying spatial autocorrelation in the data. For example, the
Gaussian covariance function is often useful for accounting for spatial
autocorrelation that is very smooth (i.e., long range spatial
dependence). See Chapter 2 in Banerjee, Carlin,
and Gelfand (2003) for a more thorough discussion of these
functions and their mathematical properties.
The default initial values for phi,
sigma.sq, and nu are all set to random values
from the prior distribution, which generally will be sufficient for the
models discussed in this vignette. In all spatially-explicit models
described in this vignette, the spatial range parameter phi
is the most sensitive to initial values. In general, the spatial range
parameter will often have poor mixing and take longer to converge than
the rest of the parameters in the model, so specifying an initial value
that is reasonably close to the resulting value can really help decrease
run times for complicated models. As an initial value for the spatial
range parameter phi, we compute the mean distance between
points in HBEF and then set it equal to 3 divided by this mean distance.
When using an exponential covariance function, \(\frac{3}{\phi}\) is the effective range, or
the distance at which the residual spatial correlation between two sites
drops to 0.05 (Banerjee, Carlin, and Gelfand
2003). Thus our initial guess for this effective range is the
average distance between sites across HBEF. As with all other
parameters, we generally recommend using the default initial values for
an initial model run, and if the model is taking a very long time to
converge you can rerun the model with initial values based on the
posterior means of estimated parameters from the initial model fit. For
the spatial variance parameter sigma.sq, we set the initial
value to 2. This corresponds to a fairly small spatial variance, which
we expect based on our previous work with this data set. Further, we set
the initial values of the latent spatial random effects at each site to
0. The initial values for these random effects has an extremely small
influence on the model results, so we generally recommend setting their
initial values to 0 as we have done here (this is also the default).
However, if you are running your model for a very long time and are
seeing very slow convergence of the MCMC chains, setting the initial
values of the spatial random effects to the mean estimates from a
previous run of the model could help reach convergence faster.
# Pair-wise distances between all sites
dist.hbef <- dist(ovenHBEF$coords)
# Exponential covariance model
cov.model <- "exponential"
# Specify list of inits
oven.inits <- list(alpha = 0,
beta = 0,
z = apply(ovenHBEF$y, 1, max, na.rm = TRUE),
sigma.sq = 2,
phi = 3 / mean(dist.hbef),
w = rep(0, nrow(ovenHBEF$y)))The next three arguments (n.batch,
batch.length, and accept.rate) are all related
to the specific type of MCMC sampler we use when we fit the model. The
spatial range parameter (and the spatial smoothness parameter if
cov.model = 'matern') are the two hardest parameters to
estimate in spatially-explicit models in spOccupancy. In
other words, you will often see slow mixing and convergence of the MCMC
chains for these parameters. To try to speed up this slow mixing and
convergence of these parameters, we use an algorithm called an adaptive
Metropolis-Hastings algorithm for all spatially-explicit models in
spOccupancy (see Roberts and
Rosenthal (2009) for more details on this algorithm). In this
approach, we break up the total number of MCMC samples into a set of
“batches”, where each batch has a specific number of MCMC samples. When
we fit a spatially-explicit model in spOccupancy, instead
of specifying the total number of MCMC samples in the
n.samples argument like we did in PGOcc(), we
must specify the total number of batches (n.batch) as well
as the number of MCMC samples each batch contains. Thus, the total
number of MCMC samples is n.batch * batch.length.
Typically, we set batch.length = 25 and then play around
with n.batch until convergence of all model parameters is
reached. We recommend setting batch.length = 25 unless you
have a specific reason to change it. Here we set
n.batch = 400 for a total of 10,000 MCMC samples in each of
3 chains. We additionally specify a burn-in period of length 2000 and a
thinning rate of 20.
batch.length <- 25
n.batch <- 400
n.burn <- 2000
n.thin <- 20
n.chains <- 3Importantly, we also need to specify an acceptance rate and a tuning
parameter for the spatial range parameter (and spatial smoothness
parameter if cov.model = 'matern'), which are both features
of the adaptive algorithm we use to sample these parameters. In this
algorithm, we propose new values for phi (and
nu), compare them to our previous values, and use a
statistical algorithm to determine if we should accept the new proposed
value or keep the old one. The accept.rate argument
specifies the ideal proportion of times we will accept the newly
proposed values for these parameters. Roberts and
Rosenthal (2009) show that if we accept new values around 43% of
the time, this will lead to optimal mixing and convergence of the MCMC
chains. Following these recommendations, we should strive for an
algorithm that accepts new values about 43% of the time. Thus, we
recommend setting accept.rate = 0.43 unless you have a
specific reason not to (this is the default value). The values specified
in the tuning argument helps control the initial values we
will propose for both phi and nu. These values
are supplied as input in the form of a list with tags phi
and nu. The initial tuning value can be any value greater
than 0, but we generally recommend starting the value out around 0.5.
This initial tuning value is closely related to the ideal (or target)
acceptance rate we specified in accept.rate. In short, the
algorithm we use is “adaptive” because the algorithm will change the
tuning values after each batch of the MCMC to yield acceptance rates
that are close to our target acceptance rate that we specified in the
accept.rate argument. Information on the acceptance rates
for phi and nu in your model will be displayed
when setting verbose = TRUE. After some initial runs of the
model, if you notice the final acceptance rate is much larger or smaller
than the target acceptance rate (accept.rate), you can then
change the initial tuning value to get closer to the target rate. While
use of this algorithm requires us to specify more arguments in
spatially-explicit models, this leads to much shorter run times compared
to a more simple approach where we do not have an “adaptive” sampling
approach, and it should thus save you time in the long haul when waiting
for these models to run. For our example here, we set the initial tuning
value to 1 after some initial exploratory runs of the model.
oven.tuning <- list(phi = 1)
# accept.rate = 0.43 by default, so we do not specify it.Priors are again specified in a list in the argument
priors. We follow standard recommendations for prior
distributions from the spatial statistics literature (Banerjee, Carlin, and Gelfand 2003). We assume
an inverse gamma prior for the spatial variance parameter
sigma.sq (the tag of which is sigma.sq.ig),
and uniform priors for the spatial decay parameter phi and
smoothness parameter nu (if using the Matern correlation
function), with the associated tags phi.unif and
nu.unif. The hyperparameters of the inverse Gamma are
passed as a vector of length two, with the first and second elements
corresponding to the shape and scale, respectively. The lower and upper
bounds of the uniform distribution are passed as a two-element vector
for the uniform priors.
As of v0.3.2, we allow users to specify a uniform prior on the
spatial variance parameter sigma.sq (using the tag
sigma.sq.unif) instead of an inverse-Gamma prior. This can
be useful in certain situations when working with a binary response
variable (which we inherently do in occupancy models), as there is a
confounding between the spatial variance parameter sigma.sq
and the occurrence intercept. This occurs as a result of the logit
transformation and a mathematical statement known as Jensen’s Inequality
(Bolker 2015). Briefly, Jensen’s
Inequality tells us that while the spatial random effects don’t
influence the mean on the logit scale (since we give them a prior with
mean 0), they do have an influence on the mean on the actual probability
scale (after back-transforming), which is what leads to potential
confounding between the spatial variance parameter and the occurrence
intercept. Generally, we have found this confounding to be
inconsequential, as the spatial structure of the random effects helps to
separate the spatial variance from the occurrence intercept. However,
there may be certain circumstances when \(\sigma^2\) is estimated to be extremely
large, and the estimate of the occurrence intercept is a very large
magnitude negative number in order to compensate. It can be helpful in
these situations to use a uniform distribution on sigma.sq
to restrict it to taking more reasonable values. We have rarely
encountered such situations, and so throughout this vignette (and in our
the vast majority of our analyses) we will use an inverse-Gamma
prior.
Note that the priors for the spatial parameters in a
spatially-explicit model must be at least weakly informative for the
model to converge (Banerjee, Carlin, and Gelfand
2003). For the inverse-Gamma prior on the spatial variance, we
typically set the shape parameter to 2 and the scale parameter equal to
our best guess of the spatial variance. The default prior hyperparameter
values for the spatial variance \(\sigma^2\) are a shape parameter of 2 and a
scale parameter of 1. This weakly informative prior suggests a prior
mean of 1 for the spatial variance, which is a moderately small amount
of spatial variation. Based on our previous work with these data, we
expected the residual spatial variation to be relatively small, and so
we use this default value and set the scale parameter below to 1. For
the spatial decay parameter, our default approach is to set the lower
and upper bounds of the uniform prior based on the minimum and maximum
distances between sites in the data. More specifically, by default we
set the lower bound to 3 / max and the upper bound to
3 / min, where min and max are
the minimum and maximum distances between sites in the data set,
respectively. This equates to a vague prior that states the spatial
autocorrelation in the data could only exist between sites that are very
close together, or could span across the entire observed study area. If
additional information is known on the extent of the spatial
autocorrelation in the data, you may place more restrictive bounds on
the uniform prior, which would reduce the amount of time needed for
adequate mixing and convergence of the MCMC chains. Here we use this
default approach, but will explicitly set the values for
transparency.
min.dist <- min(dist.hbef)
max.dist <- max(dist.hbef)
oven.priors <- list(beta.normal = list(mean = 0, var = 2.72),
alpha.normal = list(mean = 0, var = 2.72),
sigma.sq.ig = c(2, 1),
phi.unif = c(3/max.dist, 3/min.dist))The argument n.omp.threads specifies the number of
threads to use for within-chain parallelization, while
verbose specifies whether or not to print the progress of
the sampler. We highly recommend setting
verbose = TRUE for all spatial models to ensure the
adaptive MCMC is working as you want (and this is the reason for why
this is the default for this argument). The argument
n.report specifies the interval to report the
Metropolis-Hastings sampler acceptance rate. Note that
n.report is specified in terms of batches, not the overall
number of samples. Below we set n.report = 100, which will
result in information on the acceptance rate and tuning parameters every
100th batch (not sample).
n.omp.threads <- 1
verbose <- TRUE
n.report <- 100 # Report progress at every 100th batch.The parameters NNGP, n.neighbors, and
search.type relate to whether or not you want to fit the
model with a Gaussian Process or with NNGP, which is a much more
computationally efficient approximation. The argument NNGP
is a logical value indicating whether to fit the model with an NNGP
(TRUE) or a regular Gaussian Process (FALSE).
For data sets that have more than 1000 locations, using an NNGP will
have substantial improvements in run time. Even for more modest-sized
data sets, like the HBEF data set, using an NNGP will be quite a bit
faster (especially for multi-species models as shown in subsequent
sections). Unless your data set is particularly small (e.g., 100 points)
and you are concerned about the NNGP approximation, we recommend setting
NNGP = TRUE, which is the default. The arguments
n.neighbors and search.type specify the number
of neighbors used in the NNGP and the nearest neighbor search algorithm,
respectively, to use for the NNGP model. Generally, the default values
of these arguments will be adequate. Datta et al.
(2016) showed that setting n.neighbors = 15 is
usually sufficient, although for certain data sets a good approximation
can be achieved with as few as five neighbors, which could substantially
decrease run time for the model. We generally recommend leaving
search.type = "cb", as this results in a fast code book
nearest neighbor search algorithm. However, details on when you may want
to change this are described in Finley, Datta,
and Banerjee (2020). We will run an NNGP model using the default
value for search.type and setting
n.neighbors = 5, which we have found in exploratory
analysis to closely approximate a full Gaussian Process.
We now fit the model (without k-fold cross-validation) and summarize
the results using summary().
# Approx. run time: < 1 minute
out.sp <- spPGOcc(occ.formula = oven.occ.formula,
det.formula = oven.det.formula,
data = ovenHBEF,
inits = oven.inits,
n.batch = n.batch,
batch.length = batch.length,
priors = oven.priors,
cov.model = cov.model,
NNGP = TRUE,
n.neighbors = 5,
tuning = oven.tuning,
n.report = n.report,
n.burn = n.burn,
n.thin = n.thin,
n.chains = n.chains)----------------------------------------
Preparing to run the model
----------------------------------------
----------------------------------------
Building the neighbor list
----------------------------------------
----------------------------------------
Building the neighbors of neighbors list
----------------------------------------
----------------------------------------
Model description
----------------------------------------
NNGP Spatial Occupancy model with Polya-Gamma latent
variable fit with 373 sites.
Samples per chain: 10000 (400 batches of length 25)
Burn-in: 2000
Thinning Rate: 20
Number of Chains: 3
Total Posterior Samples: 1200
Using the exponential spatial correlation model.
Using 5 nearest neighbors.
Source compiled with OpenMP support and model fit using 1 thread(s).
Adaptive Metropolis with target acceptance rate: 43.0
----------------------------------------
Chain 1
----------------------------------------
Sampling ...
Batch: 100 of 400, 25.00%
Parameter Acceptance Tuning
phi 44.0 0.40252
-------------------------------------------------
Batch: 200 of 400, 50.00%
Parameter Acceptance Tuning
phi 40.0 0.28650
-------------------------------------------------
Batch: 300 of 400, 75.00%
Parameter Acceptance Tuning
phi 60.0 0.31664
-------------------------------------------------
Batch: 400 of 400, 100.00%
----------------------------------------
Chain 2
----------------------------------------
Sampling ...
Batch: 100 of 400, 25.00%
Parameter Acceptance Tuning
phi 56.0 0.29229
-------------------------------------------------
Batch: 200 of 400, 50.00%
Parameter Acceptance Tuning
phi 48.0 0.37158
-------------------------------------------------
Batch: 300 of 400, 75.00%
Parameter Acceptance Tuning
phi 40.0 0.29229
-------------------------------------------------
Batch: 400 of 400, 100.00%
----------------------------------------
Chain 3
----------------------------------------
Sampling ...
Batch: 100 of 400, 25.00%
Parameter Acceptance Tuning
phi 56.0 0.29229
-------------------------------------------------
Batch: 200 of 400, 50.00%
Parameter Acceptance Tuning
phi 44.0 0.31664
-------------------------------------------------
Batch: 300 of 400, 75.00%
Parameter Acceptance Tuning
phi 32.0 0.34301
-------------------------------------------------
Batch: 400 of 400, 100.00%
class(out.sp) # Look at what spOccupancy produced.[1] "spPGOcc"
names(out.sp) [1] "rhat" "beta.samples" "alpha.samples" "theta.samples"
[5] "coords" "z.samples" "X" "X.re"
[9] "w.samples" "psi.samples" "like.samples" "X.p"
[13] "X.p.re" "y" "ESS" "call"
[17] "n.samples" "n.neighbors" "cov.model.indx" "type"
[21] "n.post" "n.thin" "n.burn" "n.chains"
[25] "pRE" "psiRE" "run.time"
summary(out.sp)
Call:
spPGOcc(occ.formula = oven.occ.formula, det.formula = oven.det.formula,
data = ovenHBEF, inits = oven.inits, priors = oven.priors,
tuning = oven.tuning, cov.model = cov.model, NNGP = TRUE,
n.neighbors = 5, n.batch = n.batch, batch.length = batch.length,
n.report = n.report, n.burn = n.burn, n.thin = n.thin, n.chains = n.chains)
Samples per Chain: 10000
Burn-in: 2000
Thinning Rate: 20
Number of Chains: 3
Total Posterior Samples: 1200
Run Time (min): 0.5227
Occurrence (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) 2.8451 0.7525 1.2774 2.8688 4.3535 1.0169 148
scale(Elevation) -2.4890 0.5974 -3.8620 -2.4186 -1.5604 1.0630 194
I(scale(Elevation)^2) -0.6868 0.3364 -1.3461 -0.6853 0.0027 1.0142 882
Detection (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) 0.8201 0.1219 0.5760 0.8161 1.0565 1.0081 1200
scale(day) -0.0916 0.0786 -0.2511 -0.0913 0.0674 1.0094 1200
scale(tod) -0.0465 0.0773 -0.1956 -0.0485 0.1061 1.0071 1397
I(scale(day)^2) 0.0262 0.0948 -0.1540 0.0272 0.2108 1.0022 1235
Spatial Covariance:
Mean SD 2.5% 50% 97.5% Rhat ESS
sigma.sq 5.1171 3.3485 1.1532 4.2911 13.8545 1.0696 100
phi 0.0020 0.0008 0.0007 0.0019 0.0039 1.0158 160Most Rhat values are less than 1.1, although for a full analysis we
should run the model longer to ensure the spatial variance parameter
(sigma.sq) has converged. The effective sample sizes of the
spatial covariance parameters are somewhat low, which indicates limited
mixing of these parameters. This is common when fitting spatial models.
We note that there is substantial MC error in the spatial covariance
parameters, and so your estimates may be slightly different from what we
have shown here. We see spPGOcc() returns a list of class
spPGOcc and consists of posterior samples for all
parameters. Note that posterior samples for spatial parameters are
stored in the list element theta.samples.
Posterior predictive checks
For our posterior predictive check, we send the spPGOcc
model object to the ppcOcc() function, this time grouping
by replicate, or survey occasion, (group = 2) instead of by
site (group = 1).
Call:
ppcOcc(object = out.sp, fit.stat = "freeman-tukey", group = 2)
Samples per Chain: 10000
Burn-in: 2000
Thinning Rate: 20
Number of Chains: 3
Total Posterior Samples: 1200
Bayesian p-value: 0.3625
Fit statistic: freeman-tukey The Bayesian p-value indicates adequate fit of the spatial occupancy model.
Model selection using WAIC and k-fold cross-validation
We next use the waicOcc() function to compute the WAIC,
which we can compare to the non-spatial model to assess the benefit of
incorporating the spatial random effects in the occurrence model.
waicOcc(out.sp) elpd pD WAIC
-570.18590 45.58676 1231.54533
# Compare to non-spatial model
waicOcc(out) elpd pD WAIC
-632.960543 6.290149 1278.501382 We see the WAIC value for the spatial model is substantially reduced compared to the nonspatial model, indicating that incorporation of the spatial random effects yields an improvement in predictive performance.
k-fold cross-validation is accomplished by specifying the
k.fold argument in spPGOcc just as we saw in
PGOcc.
Prediction
Finally, we can perform out of sample prediction using the
predict function just as before. Prediction for spatial
models is more computationally intensive than for non-spatial models,
and so the predict function for spPGOcc class
objects also has options for parallelization
(n.omp.threads) and reporting sampler progress
(verbose and n.report). Note that for
spPGOcc(), you also need to supply the coordinates of the
out of sample prediction locations in addition to the covariate
values.
# Do prediction.
coords.0 <- as.matrix(hbefElev[, c('Easting', 'Northing')])
# Approx. run time: 6 min
out.sp.pred <- predict(out.sp, X.0, coords.0, verbose = FALSE)
# Produce a species distribution map (posterior predictive means of occupancy)
plot.dat <- data.frame(x = hbefElev$Easting,
y = hbefElev$Northing,
mean.psi = apply(out.sp.pred$psi.0.samples, 2, mean),
sd.psi = apply(out.sp.pred$psi.0.samples, 2, sd))
dat.stars <- st_as_stars(plot.dat, dims = c('x', 'y'))
ggplot() +
geom_stars(data = dat.stars, aes(x = x, y = y, fill = mean.psi)) +
scale_fill_viridis_c(na.value = 'transparent') +
labs(x = 'Easting', y = 'Northing', fill = '',
title = 'Mean OVEN occurrence probability') +
theme_bw()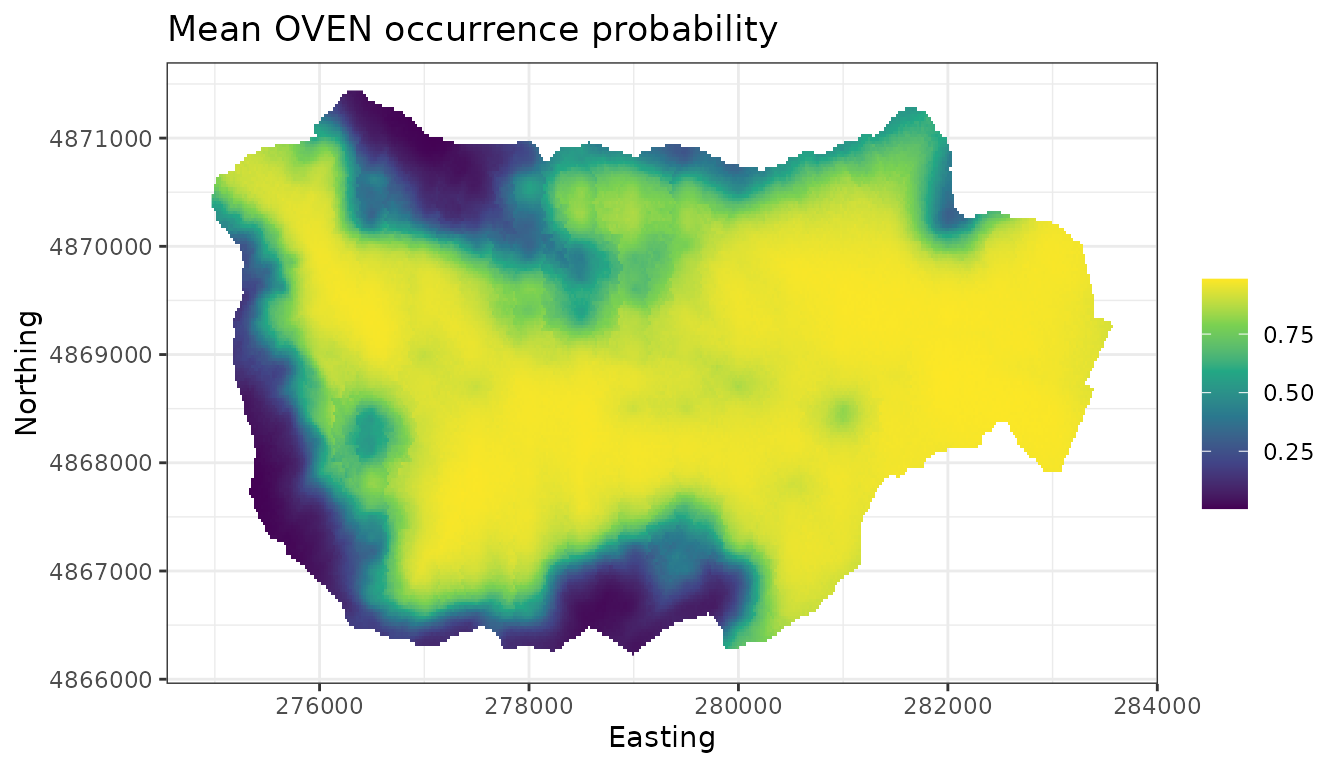
# Produce an uncertainty map of the SDM (posterior predictive SDs of occupancy)
ggplot() +
geom_stars(data = dat.stars, aes(x = x, y = y, fill = sd.psi)) +
scale_fill_viridis_c(na.value = 'transparent') +
labs(x = 'Easting', y = 'Northing', fill = '',
title = 'SD OVEN occurrence probability') +
theme_bw()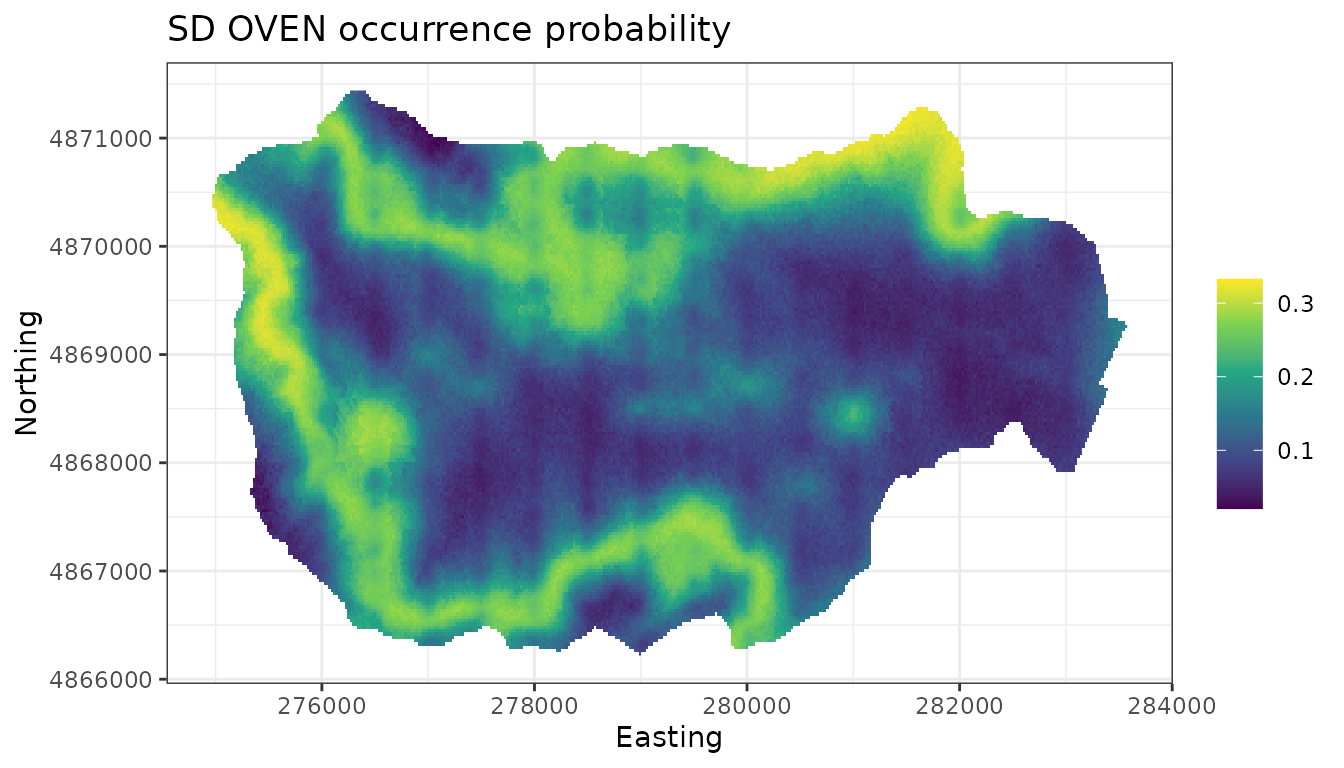
Comparing this to the non-spatial occupancy model, the spatial model appears to identify areas in HBEF with low OVEN occurrence that are not captured in the non-spatial model. We will resist trying to hypothesize what environmental factors could lead to these patterns.
Multi-species occupancy models
Basic model description
Let \(z_{i, j}\) be the true presence (1) or absence (0) of a species \(i\) at site \(j\), with \(j = 1, \dots, J\) and \(i = 1, \dots, N\). We assume the latent occurrence variable arises from a Bernoulli process following
\[\begin{equation} \begin{split} &z_{i, j} \sim \text{Bernoulli}(\psi_{i, j}), \\ &\text{logit}(\psi_{i, j}) = \boldsymbol{x}^{\top}_{j}\boldsymbol{\beta}_i, \end{split} \end{equation}\]
where \(\psi_{i, j}\) is the probability of occurrence of species \(i\) at site \(j\), which is a function of site-specific covariates \(\boldsymbol{X}\) and a vector of species-specific regression coefficients (\(\boldsymbol{\beta}_i\)). The regression coefficients in multi-species occupancy models are envisioned as random effects arising from a common community level distribution:
\[\begin{equation} \boldsymbol{\beta}_i \sim \text{Normal}(\boldsymbol{\mu}_{\beta}, \boldsymbol{T}_{\beta}), \end{equation}\]
where \(\boldsymbol{\mu}_{\beta}\) is a vector of community level mean effects for each occurrence covariate effect (including the intercept) and \(\boldsymbol{T}_{\beta}\) is a diagonal matrix with diagonal elements \(\boldsymbol{\tau}^2_{\beta}\) that represent the variability of each occurrence covariate effect among species in the community.
We do not directly observe \(z_{i, j}\), but rather we observe an imperfect representation of the latent occurrence process. Let \(y_{i, j, k}\) be the observed detection (1) or nondetection (0) of a species \(i\) at site \(j\) during replicate/survey \(k\) for each of \(k = 1, \dots, K_j\) replicates at each site \(j\). We envision the detection-nondetection data as arising from a Bernoulli process conditional on the true latent occurrence process:
\[\begin{equation} \begin{split} &y_{i, j, k} \sim \text{Bernoulli}(p_{i, j, k}z_{i, j}), \\ &\text{logit}(p_{i, j, k}) = \boldsymbol{v}^{\top}_{i, j, k}\boldsymbol{\alpha}_i, \end{split} \end{equation}\]
where \(p_{i, j, k}\) is the probability of detecting species \(i\) at site \(j\) during replicate \(k\) (given it is present at site \(j\)), which is a function of site and replicate specific covariates \(\boldsymbol{V}\) and a vector of species-specific regression coefficients (\(\boldsymbol{\alpha}_i\)). Similarly to the occurrence regression coefficients, the species specific detection coefficients are envisioned as random effects arising from a common community level distribution:
\[\begin{equation} \boldsymbol{\alpha}_i \sim \text{Normal}(\boldsymbol{\mu}_{\alpha}, \boldsymbol{T}_{\alpha}), \end{equation}\]
where \(\boldsymbol{\mu}_{\alpha}\) is a vector of community level mean effects for each detection covariate effect (including the intercept) and \(\boldsymbol{T}_{\alpha}\) is a diagonal matrix with diagonal elements \(\boldsymbol{\tau}^2_{\alpha}\) that represent the variability of each detection covariate effect among species in the community.
To complete the Bayesian specification of the model, we assign multivariate normal priors for the occurrence (\(\boldsymbol{\mu}_{\beta}\)) and detection (\(\boldsymbol{\mu}_{\alpha}\)) community-level regression coefficient means and independent inverse-Gamma priors for each element of \(\boldsymbol{\tau}^2_{\beta}\) and \(\boldsymbol{\tau}^2_{\alpha}\). We again use Pólya-Gamma data augmentation to yield an efficient implementation of the multi-species occupancy model, which is described in depth in the MCMC sampler vignette.
Fitting multi-species occupancy models with
msPGOcc()
spOccupancy uses nearly identical syntax for fitting
multi-species occupancy models as it does for single-species models and
provides the same functionality for posterior predictive checks, model
assessment and selection using WAIC and k-fold cross-validation, and out
of sample prediction. The msPGOcc() function fits
nonspatial multi-species occupancy models using Pólya-Gamma latent
variables, which results in substantial increases in run time compared
to standard implementations of logit link multi-species occupancy
models. msPGOcc() has exactly the same arguments as
PGOcc():
msPGOcc(occ.formula, det.formula, data, inits, n.samples, priors,
n.omp.threads = 1, verbose = TRUE, n.report = 100,
n.burn = round(.10 * n.samples), n.thin = 1, n.chains = 1,
k.fold, k.fold.threads = 1, k.fold.seed, k.fold.only = FALSE, ...)For illustration, we will again use the Hubbard Brook data in
hbef2015, but we will now model occurrence for all 12
species in the community. Below we reload the hbef2015 data
set to get a fresh copy.
data(hbef2015)
# str(hbef2015) # Remind ourselves of what's in it (not shown).We will model occurrence for all species as a function of linear and
quadratic terms for elevation, and detection as a function of linear and
quadratic day of survey as well as the time of day during which the
survey was conducted. These models are specified in
occ.formula and det.formula as before, which
reference variables stored in the data list. Random
intercepts can be included in both the occurrence and detection portions
of the occupancy model using lme4 syntax (Bates et al. 2015). For multi-species models,
the multi-species detection-nondetection data y is now a
three-dimensional array with dimensions corresponding to species, sites,
and replicates. This is how the data are provided in the
hbef2015 object, so we don’t need to do any additional
preparations.
occ.ms.formula <- ~ scale(Elevation) + I(scale(Elevation)^2)
det.ms.formula <- ~ scale(day) + scale(tod) + I(scale(day)^2)
str(hbef2015)List of 4
$ y : num [1:12, 1:373, 1:3] 0 0 0 0 0 1 0 0 0 0 ...
..- attr(*, "dimnames")=List of 3
.. ..$ : chr [1:12] "AMRE" "BAWW" "BHVI" "BLBW" ...
.. ..$ : chr [1:373] "1" "2" "3" "4" ...
.. ..$ : chr [1:3] "1" "2" "3"
$ occ.covs: num [1:373, 1] 475 494 546 587 588 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : NULL
.. ..$ : chr "Elevation"
$ det.covs:List of 2
..$ day: num [1:373, 1:3] 156 156 156 156 156 156 156 156 156 156 ...
..$ tod: num [1:373, 1:3] 330 346 369 386 409 425 447 463 482 499 ...
$ coords : num [1:373, 1:2] 280000 280000 280000 280001 280000 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:373] "1" "2" "3" "4" ...
.. ..$ : chr [1:2] "X" "Y"Next we specify the initial values in inits. For
multi-species occupancy models, we supply initial values for
community-level and species-level parameters. In msPGOcc(),
we will supply initial values for the following parameters:
alpha.comm (community-level detection coefficients),
beta.comm (community-level occurrence coefficients),
alpha (species-level detection coefficients),
beta (species-level occurrence coefficients),
tau.sq.beta (community-level occurrence variance
parameters), tau.sq.alpha (community-level detection
variance parameters, z (latent occurrence variables for all
species). These are all specified in a single list. Initial values for
community-level parameters are either vectors of length corresponding to
the number of community-level detection or occurrence parameters in the
model (including the intercepts) or a single value if all parameters are
assigned the same initial values. Initial values for species level
parameters are either matrices with the number of rows indicating the
number of species, and each column corresponding to a different
regression parameter, or a single value if the same initial value is
used for all species and parameters. The initial values for the latent
occurrence matrix are specified as a matrix with \(N\) rows corresponding to the number of
species and \(J\) columns corresponding
to the number of sites.
N <- dim(hbef2015$y)[1]
ms.inits <- list(alpha.comm = 0,
beta.comm = 0,
beta = 0,
alpha = 0,
tau.sq.beta = 1,
tau.sq.alpha = 1,
z = apply(hbef2015$y, c(1, 2), max, na.rm = TRUE))In multi-species models, we specify priors on the community-level
coefficients (or hyperparameters) rather than the species-level effects.
For nonspatial models, these priors are specified with the following
tags: beta.comm.normal (normal prior on the community-level
occurrence mean effects), alpha.comm.normal (normal prior
on the community-level detection mean effects),
tau.sq.beta.ig (inverse-Gamma prior on the community-level
occurrence variance parameters), tau.sq.alpha.ig
(inverse-Gamma prior on the community-level detection variance
parameters). Each tag consists of a list with elements corresponding to
the mean and variance for normal priors and scale and shape for
inverse-Gamma priors. Values can be specified individually for each
parameter or as a single value if the same prior is assigned to all
parameters of a given type.
By default, we set the prior hyperparameter values for the community-level means to a mean of 0 and a variance of 2.72, which results in a vague prior on the probability scale as we discussed for the single-species spatial occupancy model. Below we specify these priors explicitly. For the community-level variance parameters, by default we set the scale and shape parameters to 0.1 following the recommendations of (Lunn et al. 2013), which results in a weakly informative prior on the community-level variances. This may lead to shrinkage of the community-level variance towards zero under certain circumstances so that all species will have fairly similar values for the species-specific covariate effect (Gelman 2006), although we have found multi-species occupancy models to be relatively robust to this prior specification. However, if you want to explore the impact of this prior on species-specific covariate effects, we recommend running single-species occupancy models for a select number of species in the data set, and assessing how large the differences in the estimated species-specific effects are between the single-species model estimates and those from the multi-species model. Below we explicitly set these default prior values for our HBEF example.
ms.priors <- list(beta.comm.normal = list(mean = 0, var = 2.72),
alpha.comm.normal = list(mean = 0, var = 2.72),
tau.sq.beta.ig = list(a = 0.1, b = 0.1),
tau.sq.alpha.ig = list(a = 0.1, b = 0.1))All that’s now left to do is specify the number of threads to use
(n.omp.threads), the number of MCMC samples
(n.samples), the amount of samples to discard as burn-in
(n.burn), the thinning rate (n.thin), and
arguments to control the display of sampler progress
(verbose, n.report).
# Approx. run time: 6 min
out.ms <- msPGOcc(occ.formula = occ.ms.formula,
det.formula = det.ms.formula,
data = hbef2015,
inits = ms.inits,
n.samples = 30000,
priors = ms.priors,
n.omp.threads = 1,
verbose = TRUE,
n.report = 6000,
n.burn = 10000,
n.thin = 50,
n.chains = 3)----------------------------------------
Preparing to run the model
----------------------------------------
----------------------------------------
Model description
----------------------------------------
Multi-species Occupancy Model with Polya-Gamma latent
variable fit with 373 sites and 12 species.
Samples per Chain: 30000
Burn-in: 10000
Thinning Rate: 50
Number of Chains: 3
Total Posterior Samples: 1200
Source compiled with OpenMP support and model fit using 1 thread(s).
----------------------------------------
Chain 1
----------------------------------------
Sampling ...
Sampled: 6000 of 30000, 20.00%
-------------------------------------------------
Sampled: 12000 of 30000, 40.00%
-------------------------------------------------
Sampled: 18000 of 30000, 60.00%
-------------------------------------------------
Sampled: 24000 of 30000, 80.00%
-------------------------------------------------
Sampled: 30000 of 30000, 100.00%
----------------------------------------
Chain 2
----------------------------------------
Sampling ...
Sampled: 6000 of 30000, 20.00%
-------------------------------------------------
Sampled: 12000 of 30000, 40.00%
-------------------------------------------------
Sampled: 18000 of 30000, 60.00%
-------------------------------------------------
Sampled: 24000 of 30000, 80.00%
-------------------------------------------------
Sampled: 30000 of 30000, 100.00%
----------------------------------------
Chain 3
----------------------------------------
Sampling ...
Sampled: 6000 of 30000, 20.00%
-------------------------------------------------
Sampled: 12000 of 30000, 40.00%
-------------------------------------------------
Sampled: 18000 of 30000, 60.00%
-------------------------------------------------
Sampled: 24000 of 30000, 80.00%
-------------------------------------------------
Sampled: 30000 of 30000, 100.00%The resulting object out.ms is a list of class
msPGOcc() consisting primarily of posterior samples of all
community and species-level parameters, as well as some additional
objects that are used for summaries, prediction, and model fit
evaluation. We can display a nice summary of these results using the
summary() function as before. For multi-species objects,
when using summary we need to specify the level of parameters we want to
summarize. We do this using the argument level, which takes
values community, species, or
both to print results for community-level parameters,
species-level parameters, or all parameters. By default,
level is set to both to display both species
and community-level parameters.
summary(out.ms)
Call:
msPGOcc(occ.formula = occ.ms.formula, det.formula = det.ms.formula,
data = hbef2015, inits = ms.inits, priors = ms.priors, n.samples = 30000,
n.omp.threads = 1, verbose = TRUE, n.report = 6000, n.burn = 10000,
n.thin = 50, n.chains = 3)
Samples per Chain: 30000
Burn-in: 10000
Thinning Rate: 50
Number of Chains: 3
Total Posterior Samples: 1200
Run Time (min): 3.7973
----------------------------------------
Community Level
----------------------------------------
Occurrence Means (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) 0.3987 0.8466 -1.2355 0.4173 2.0355 0.9999 695
scale(Elevation) 0.2502 0.5167 -0.7423 0.2656 1.2784 1.0041 995
I(scale(Elevation)^2) -0.2058 0.2591 -0.7057 -0.2083 0.3267 1.0041 547
Occurrence Variances (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) 11.1212 6.0429 4.2431 9.6963 26.3994 1.0086 801
scale(Elevation) 3.1125 1.8713 1.0216 2.6385 8.0685 1.0235 533
I(scale(Elevation)^2) 0.5995 0.4476 0.1406 0.4800 1.7667 1.0074 1001
Detection Means (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) -0.8073 0.4771 -1.8299 -0.7842 0.0581 1.0104 1088
scale(day) 0.0547 0.0900 -0.1264 0.0609 0.2259 1.0081 1200
scale(tod) -0.0392 0.0765 -0.1809 -0.0420 0.1163 1.0002 1200
I(scale(day)^2) -0.0283 0.0823 -0.1949 -0.0275 0.1218 1.0019 1200
Detection Variances (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) 2.7869 1.6052 0.9394 2.3628 7.0023 1.0129 266
scale(day) 0.0670 0.0366 0.0244 0.0582 0.1553 1.0125 1462
scale(tod) 0.0488 0.0325 0.0158 0.0406 0.1231 1.0288 1200
I(scale(day)^2) 0.0567 0.0408 0.0171 0.0464 0.1738 1.0059 1200
----------------------------------------
Species Level
----------------------------------------
Occurrence (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept)-AMRE -1.5597 2.2597 -4.5866 -2.1403 4.1002 1.0521 55
(Intercept)-BAWW 2.2766 1.6257 -0.0343 2.0245 6.0780 1.0279 172
(Intercept)-BHVI 3.4291 2.3885 0.1024 3.0350 8.6017 1.0325 138
(Intercept)-BLBW 2.5933 0.7706 1.6771 2.4543 4.3684 1.0389 183
(Intercept)-BLPW -4.6809 0.6293 -6.0543 -4.6335 -3.6021 1.0102 807
(Intercept)-BTBW 3.6292 0.5009 2.7981 3.5717 4.7210 1.0082 1200
(Intercept)-BTNW 2.4408 0.3546 1.8625 2.3997 3.3232 1.0062 1097
(Intercept)-CAWA -2.1821 0.5661 -3.1573 -2.2361 -0.9341 1.0222 642
(Intercept)-MAWA -1.7142 0.2550 -2.2061 -1.7206 -1.2088 1.0014 1302
(Intercept)-NAWA -2.4934 0.5829 -3.5619 -2.5385 -1.2062 1.0105 742
(Intercept)-OVEN 2.1568 0.2785 1.6567 2.1377 2.7453 1.0076 1482
(Intercept)-REVI 3.1456 0.4802 2.3854 3.0958 4.2352 1.0013 713
scale(Elevation)-AMRE 1.0837 1.2523 -0.8191 0.9139 4.1875 1.0038 103
scale(Elevation)-BAWW -0.7963 1.2628 -4.1075 -0.5926 1.8835 1.0374 142
scale(Elevation)-BHVI 0.1307 1.0588 -2.0938 0.1832 2.1846 1.0407 586
scale(Elevation)-BLBW -0.4674 0.4682 -1.1844 -0.3988 -0.0389 1.1283 137
scale(Elevation)-BLPW 2.7121 0.6709 1.7122 2.6163 4.3331 1.0052 810
scale(Elevation)-BTBW -0.4832 0.1773 -0.8401 -0.4756 -0.1458 1.0003 1200
scale(Elevation)-BTNW 0.6695 0.2796 0.2180 0.6366 1.3011 1.0064 1200
scale(Elevation)-CAWA 1.8401 0.6173 0.8792 1.7535 3.2695 1.0093 986
scale(Elevation)-MAWA 1.5641 0.2697 1.0469 1.5543 2.1000 1.0109 1200
scale(Elevation)-NAWA 1.1564 0.3858 0.5169 1.1249 2.0360 1.0139 1021
scale(Elevation)-OVEN -1.6765 0.2941 -2.3842 -1.6366 -1.2210 1.0013 1200
scale(Elevation)-REVI -2.1586 0.7183 -3.7736 -2.0408 -1.1218 0.9996 628
I(scale(Elevation)^2)-AMRE -0.6034 0.6763 -2.0106 -0.5883 0.7993 1.0101 356
I(scale(Elevation)^2)-BAWW -0.9389 0.5443 -1.9675 -0.9518 0.2881 1.0348 227
I(scale(Elevation)^2)-BHVI 0.3985 0.7343 -0.8426 0.3251 2.1021 1.0047 690
I(scale(Elevation)^2)-BLBW -0.5574 0.1914 -0.9702 -0.5537 -0.2315 1.0054 808
I(scale(Elevation)^2)-BLPW 0.7545 0.3925 -0.0538 0.7753 1.4671 1.0110 975
I(scale(Elevation)^2)-BTBW -1.0239 0.1723 -1.3800 -1.0166 -0.7067 1.0019 1200
I(scale(Elevation)^2)-BTNW -0.1342 0.1720 -0.4296 -0.1439 0.2434 1.0024 1289
I(scale(Elevation)^2)-CAWA -0.4944 0.4208 -1.3114 -0.4877 0.3475 1.0044 936
I(scale(Elevation)^2)-MAWA 0.3028 0.2301 -0.1439 0.3044 0.7673 1.0110 1200
I(scale(Elevation)^2)-NAWA 0.2862 0.2724 -0.2236 0.2815 0.8261 1.0281 1200
I(scale(Elevation)^2)-OVEN -0.4200 0.1941 -0.7838 -0.4338 -0.0056 1.0117 967
I(scale(Elevation)^2)-REVI -0.0177 0.3665 -0.6200 -0.0504 0.7668 1.0027 696
Detection (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept)-AMRE -3.0777 1.4737 -5.6443 -3.0510 -0.4770 1.0165 84
(Intercept)-BAWW -2.7345 0.3782 -3.3958 -2.7905 -1.9038 1.0211 309
(Intercept)-BHVI -2.7210 0.2252 -3.1261 -2.7319 -2.2565 1.0038 433
(Intercept)-BLBW -0.0420 0.1254 -0.2852 -0.0444 0.2022 1.0016 715
(Intercept)-BLPW -0.4538 0.2605 -0.9558 -0.4547 0.0606 1.0173 1200
(Intercept)-BTBW 0.6399 0.1117 0.4224 0.6381 0.8596 1.0027 1200
(Intercept)-BTNW 0.5837 0.1115 0.3778 0.5788 0.8230 1.0081 1200
(Intercept)-CAWA -1.5175 0.5263 -2.6254 -1.5011 -0.5716 1.0217 705
(Intercept)-MAWA -0.7799 0.2336 -1.2287 -0.7851 -0.3075 1.0067 1200
(Intercept)-NAWA -1.5307 0.5206 -2.5858 -1.5124 -0.5754 1.0084 785
(Intercept)-OVEN 0.7983 0.1177 0.5774 0.7989 1.0331 1.0092 1200
(Intercept)-REVI 0.5466 0.1072 0.3394 0.5445 0.7691 1.0068 1200
scale(day)-AMRE 0.0371 0.2352 -0.4406 0.0400 0.5290 1.0070 1200
scale(day)-BAWW 0.2202 0.1365 -0.0396 0.2144 0.5013 1.0203 1200
scale(day)-BHVI 0.1966 0.1186 -0.0289 0.1966 0.4461 1.0047 1200
scale(day)-BLBW -0.2228 0.0689 -0.3573 -0.2205 -0.0876 1.0047 1080
scale(day)-BLPW 0.0737 0.1571 -0.2154 0.0729 0.3895 1.0045 1263
scale(day)-BTBW 0.2709 0.0680 0.1371 0.2734 0.4037 1.0040 1200
scale(day)-BTNW 0.1501 0.0665 0.0229 0.1502 0.2809 1.0114 1200
scale(day)-CAWA -0.0192 0.1805 -0.3712 -0.0185 0.3304 1.0014 1200
scale(day)-MAWA 0.1139 0.1254 -0.1363 0.1168 0.3570 1.0037 1202
scale(day)-NAWA 0.0128 0.1815 -0.3356 0.0132 0.3804 1.0236 1200
scale(day)-OVEN -0.0757 0.0750 -0.2281 -0.0757 0.0748 1.0118 1200
scale(day)-REVI -0.0701 0.0667 -0.2098 -0.0676 0.0550 1.0022 1200
scale(tod)-AMRE -0.0330 0.2074 -0.4553 -0.0318 0.4005 1.0006 1087
scale(tod)-BAWW -0.1839 0.1366 -0.4547 -0.1860 0.0726 1.0046 949
scale(tod)-BHVI -0.0465 0.1099 -0.2589 -0.0482 0.1705 0.9999 1329
scale(tod)-BLBW 0.0553 0.0643 -0.0638 0.0528 0.1888 1.0019 1200
scale(tod)-BLPW 0.1130 0.1484 -0.1659 0.1135 0.4079 1.0028 1200
scale(tod)-BTBW -0.0327 0.0649 -0.1572 -0.0316 0.0924 1.0114 1200
scale(tod)-BTNW 0.0368 0.0628 -0.0898 0.0356 0.1591 1.0013 1200
scale(tod)-CAWA -0.1990 0.1692 -0.5447 -0.1959 0.1129 1.0005 1200
scale(tod)-MAWA 0.0185 0.1140 -0.1945 0.0182 0.2406 1.0014 1200
scale(tod)-NAWA -0.0707 0.1576 -0.3801 -0.0702 0.2536 1.0036 1200
scale(tod)-OVEN -0.0452 0.0710 -0.1884 -0.0436 0.0915 1.0014 1545
scale(tod)-REVI -0.0780 0.0669 -0.2135 -0.0757 0.0519 1.0017 1200
I(scale(day)^2)-AMRE -0.1190 0.2186 -0.5914 -0.1063 0.2853 1.0071 1200
I(scale(day)^2)-BAWW -0.0334 0.1435 -0.3156 -0.0318 0.2496 1.0105 1200
I(scale(day)^2)-BHVI 0.0546 0.1270 -0.1885 0.0451 0.3055 1.0016 1200
I(scale(day)^2)-BLBW -0.1730 0.0792 -0.3347 -0.1733 -0.0240 1.0019 1200
I(scale(day)^2)-BLPW 0.1857 0.1844 -0.1761 0.1853 0.5530 1.0010 1107
I(scale(day)^2)-BTBW -0.0629 0.0815 -0.2305 -0.0629 0.1046 1.0000 1200
I(scale(day)^2)-BTNW -0.0643 0.0767 -0.2120 -0.0639 0.0840 1.0052 1200
I(scale(day)^2)-CAWA -0.0402 0.1873 -0.4298 -0.0400 0.3176 1.0001 1200
I(scale(day)^2)-MAWA 0.0131 0.1412 -0.2540 0.0154 0.2887 1.0048 1200
I(scale(day)^2)-NAWA -0.1308 0.1867 -0.5027 -0.1247 0.2368 1.0108 1200
I(scale(day)^2)-OVEN 0.0171 0.0846 -0.1535 0.0161 0.1861 1.0134 1200
I(scale(day)^2)-REVI 0.0393 0.0789 -0.1152 0.0358 0.1930 1.0015 1200
# Or more explicitly
# summary(out.ms, level = 'both')Looking at the community-level variance parameters, we see substantial variability in the average occurrence (the intercept) for the twelve species, as well as considerable variability in the effect of elevation across the community. There appears to be less variability across species in the detection portion of the model. We can look directly at the species-specific effects to confirm this. All community-level Rhat values are less than 1.1 and most species-level Rhat values are less than 1.1, with the exception of a few of the parameters for rare species. Mixing of the MCMC chains appears adequate when looking at the ESS values, although we can clearly see the ESS is lower for rare species (e.g., AMRE, BAWW) compared to more common species in the forest (e.g., OVEN, REVI).
Posterior predictive checks
We can use the ppcOcc() function to perform a posterior
predictive check, and summarize the check with a Bayesian p-value using
the summary() function, all as shown before. The
summary() function again requires the level
argument to specify if you want an overall Bayesian p-value for the
entire community (level = 'community'), each individual
species (level = 'species'), or for both
(level = 'both'). By default, we set `level = ‘both’.
# Approx. run time: 20 sec
ppc.ms.out <- ppcOcc(out.ms, 'chi-squared', group = 1)Currently on species 1 out of 12Currently on species 2 out of 12Currently on species 3 out of 12Currently on species 4 out of 12Currently on species 5 out of 12Currently on species 6 out of 12Currently on species 7 out of 12Currently on species 8 out of 12Currently on species 9 out of 12Currently on species 10 out of 12Currently on species 11 out of 12Currently on species 12 out of 12
summary(ppc.ms.out)
Call:
ppcOcc(object = out.ms, fit.stat = "chi-squared", group = 1)
Samples per Chain: 30000
Burn-in: 10000
Thinning Rate: 50
Number of Chains: 3
Total Posterior Samples: 1200
----------------------------------------
Community Level
----------------------------------------
Bayesian p-value: 0.3647
----------------------------------------
Species Level
----------------------------------------
AMRE Bayesian p-value: 0.5958
BAWW Bayesian p-value: 0.6367
BHVI Bayesian p-value: 0.5567
BLBW Bayesian p-value: 0.1008
BLPW Bayesian p-value: 0.6308
BTBW Bayesian p-value: 0.2242
BTNW Bayesian p-value: 0.0408
CAWA Bayesian p-value: 0.4583
MAWA Bayesian p-value: 0.4733
NAWA Bayesian p-value: 0.52
OVEN Bayesian p-value: 0.055
REVI Bayesian p-value: 0.0842
Fit statistic: chi-squared The Bayesian p-value for the overall community suggests an adequate model fit, but we see clear variation in the values for each individual species. We should explore this further in a complete analysis.
Model selection using WAIC and k-fold cross-validation
We can compute the WAIC for comparison with alternative models using
the waicOcc() function.
waicOcc(out.ms) elpd pD WAIC
-4531.90069 65.73988 9195.28116 As of v0.7.0, the waicOcc() function also
contains the argument by.sp for all multi-species models
supported by spOccupancy, which allows us to calculate WAIC
individually for each species.
waicOcc(out.ms, by.sp = TRUE) elpd pD WAIC
1 -25.99821 2.077357 56.15113
2 -176.76426 5.644309 364.81713
3 -247.35736 3.961816 502.63835
4 -705.05523 7.323082 1424.75662
5 -139.52763 5.192069 289.43940
6 -699.31982 6.878930 1412.39750
7 -730.72192 6.556928 1474.55769
8 -107.98079 4.840212 225.64201
9 -261.84192 5.430174 534.54419
10 -106.69834 5.687815 224.77232
11 -632.92884 5.813987 1277.48565
12 -697.70637 6.333204 1408.07916Note that the sum of the WAIC values for each individual species is equal to the overall WAIC value for the model.
k-fold cross-validation is again accomplished using the
k.fold argument as we have seen previously. For
multi-species occupancy models, using multiple threads can greatly
reduce the time needed for k-fold cross-validation, so we encourage the
use of multiple threads if such computing power is readily available.
Using up to \(k\) threads will
generally involve substantial decreases in run time. For multi-species
models, a separate deviance measure is reported for each species as a
measure of predictive capacity, allowing for comparisons across multiple
models for individual species, as well as for the entire community (by
summing all species-specific values).
Multi-species spatial occupancy models
Here we describe a basic multi-species spatial occupancy model that
was part of the original release of spOccupancy. Since
then, we have implemented a more computationally efficient approach for
fitting spatial multi-species occupancy models. We call this alternative
approach a “spatial factor multi-species occupancy model”, and we
describe this in depth in Doser, Finley, and
Banerjee (2023). This newer approach also accounts for residual
species correlations (i.e., it is a joint species distribution model
with imperfect detection). Our simulation results from Doser, Finley, and Banerjee (2023) show that
this alternative approach outperforms, or performs equally as well as,
the model described in the following section, while being substantially
faster. Thus, we encourage you to explore the spOccupancy
functionality to fit the spatial factor multi-species occupancy model
with the function sfMsPGOcc() that is described in
depth in this vignette. The model and function we describe below
will generally work well for communities comprised of a moderate number
of species (e.g., between 5 and 10) that are not extremely rare.
Basic model description
Residual spatial autocorrelation may perhaps be more prominent in multi-species occupancy models compared to single-species models, as a single set of covariates is used to explain occurrence probability across a region of interest for every one of the species in the modeled community. Given the large variety individual species show in habitat requirements, this may result in important drivers of occurrence probability not being included for certain species, resulting in many species having high residual spatial autocorrelation. We extend the previous multi-species occupancy model to incorporate a distinct spatial Gaussian Process (GP) for each species that accounts for unexplained spatial variation in each individual species occurrence across a spatial region. Occurrence probability for species \(i\) at site \(j\) with spatial coordinates \(\boldsymbol{s}_j\), \(\psi_{i}(\boldsymbol{s}_j)\), now takes the form
\[\begin{equation} \text{logit}(\psi_{i}(\boldsymbol{s}_j)) = \boldsymbol{x}^{\top}(\boldsymbol{s}_j)\boldsymbol{\beta}_i + \omega_{i}(\boldsymbol{s}_j), \end{equation}\]
where the species-specific regression coefficients \(\boldsymbol{\beta}_i\) follow the community-level distribution described previously for nonspatial multi-species occupancy models, and \(\omega_{i}(\boldsymbol{s}_j)\) is a realization from a zero-mean spatial GP, i.e.,
\[\begin{equation} \boldsymbol{\omega}_{i}(\boldsymbol{s}) \sim \text{Normal}(\boldsymbol{0}, \boldsymbol{\Sigma}_i(\boldsymbol{s}, \boldsymbol{s}', \boldsymbol{\theta}_i)). \end{equation}\]
We define \(\boldsymbol{\Sigma}_i(\boldsymbol{s}, \boldsymbol{s}', \boldsymbol{\theta}_i)\) as a \(J \times J\) covariance matrix that is a function of the distances between any pair of site coordinates \(\boldsymbol{s}\) and \(\boldsymbol{s}'\) and a set of parameters \((\boldsymbol{\theta}_i)\) that govern the spatial process. The vector \(\boldsymbol{\theta}_i\) is equal to \(\boldsymbol{\theta}_i = \{\sigma^2_i, \phi_i, \nu_i\}\), where \(\sigma^2_i\) is a spatial variance parameter for species \(i\), \(\phi_i\) is a spatial decay parameter for species \(i\), and \(\nu_i\) is a spatial smoothness parameter for species \(i\), where as before, \(\nu_i\) is only specified when using a Matern correlation function.
The detection portion of the multi-species spatial occupancy model remains unchanged from the non-spatial multi-species occupancy model. We fit the model again using Pólya-Gamma data augmentation to enable an efficient Gibbs sampler (see MCMC sampler vignette for details). Similar to our discussion on the single-species spatial occupancy model, we also allow for specification of the spatial process using an NNGP instead of a full GP. This leads to even larger computational gains over the full GP than in the case of a single-species model, given that a separate covariance matrix is specified for each species in the model. See Datta et al. (2016), Finley, Datta, and Banerjee (2020), and the MCMC sampler vignette for additional details on NNGPs and their implementation in multi-species spatial occupancy models.
Fitting multi-species spatial occupancy models with
spMsPGOcc()
The function spMsPGOcc() fits spatially explicit
multi-species occupancy models. Similar to single-species models using
spPGOcc(), models can be fit using either a full Gaussian
Process (GP) or a Nearest Neighbor Gaussian Process (NNGP).
spMsPGOcc() fits a separate spatial process for each
species. The syntax for spMsPGOcc() is analogous to the
syntax for single-species spatially-explicit models using
spPGOcc().
spMsPGOcc(occ.formula, det.formula, data, inits, n.batch,
batch.length, accept.rate = 0.43, priors,
cov.model = "exponential", tuning, n.omp.threads = 1,
verbose = TRUE, NNGP = TRUE, n.neighbors = 15,
search.type = "cb", n.report = 100,
n.burn = round(.10 * n.batch * batch.length), n.thin = 1,
n.chains = 1, k.fold, k.fold.threads = 1, k.fold.seed, k.fold.only = FALSE, ...)We will again showcase the model using the HBEF foliage-gleaning bird data set, with the same predictors in our occurrence and detection models
occ.ms.sp.formula <- ~ scale(Elevation) + I(scale(Elevation)^2)
det.ms.sp.formula <- ~ scale(day) + scale(tod) + I(scale(day)^2)Our initial values in the inits argument will look
analogous to what we had specified for the nonspatial multi-species
occupancy model using msPGOcc(), but we will now also
include additional initial values for the parameters controlling the
spatial processes: sigma.sq is the species-specific spatial
variance parameter, phi is the species specific spatial
decay parameter, and w is the latent spatial process for
each species at each site. We will use an exponential covariance model,
but note that when using a Matern covariance model we must also specify
initial values for nu, the species-specific spatial
smoothness parameter. Note that all species-specific spatial parameters
are independent of each other. We currently do not leverage any
correlation between spatial processes of different species, although
this is something we plan to incorporate for future
spOccupancy development. Initial values for
phi, sigma.sq, and nu (if
applicable) are specified as vectors with \(N\) elements (the number of species being
modeled) or as a single value that is used for all species, while the
initial values for the latent spatial processes are specified as a
matrix with \(N\) rows (i.e., species)
and \(J\) columns (i.e., sites). Here
we set the initial value for the spatial variances equal to 2 for all
species and set the initial values for the spatial decay parameter to
yield an effective range of the average distance between sites across
the HBEF.
# Number of species
N <- dim(hbef2015$y)[1]
# Distances between sites
dist.hbef <- dist(hbef2015$coords)
# Exponential covariance model
cov.model <- "exponential"
ms.inits <- list(alpha.comm = 0,
beta.comm = 0,
beta = 0,
alpha = 0,
tau.sq.beta = 1,
tau.sq.alpha = 1,
z = apply(hbef2015$y, c(1, 2), max, na.rm = TRUE),
sigma.sq = 2,
phi = 3 / mean(dist.hbef),
w = matrix(0, N, dim(hbef2015$y)[2]))We next specify the priors in the priors argument. The
priors are the same as those we specified for the non-spatial
multi-species model, with the addition of priors for the parameters
controlling the species-specific spatial processes. We assume
independent priors for all spatial parameters across the different
species. Priors (and their default values in spOccupancy)
for the spatial parameters are exactly analogous to those we saw for the
single-species spatially-explicit occupancy model. For each species, we
assign an inverse gamma prior for the spatial variance parameter
sigma.sq (tag is sigma.sq.ig). As of v0.3.2,
we can also specify a uniform prior for the spatial variance parameter
with tag sigma.sq.unif (see relevant discussion in
single-species spatial occupancy models). We assign uniform priors for
the spatial decay parameter phi and smoothness parameter
nu (if cov.model = 'matern'), with the
associated tags phi.unif and nu.unif. All
priors are specified as lists with two elements. For the inverse-Gamma
prior, the first element is a length \(N\) vector of shape parameters for each
species, and the second element is a length \(N\) vector of scale parameters for each
species. As we have seen many times before, if the same prior is used
for all species, both elements can be specified as single values. For
the uniform priors, the first element is a length \(N\) vector of the lower bounds for each
species, and the second element is a length \(N\) vector of upper bounds for each
species. If the same prior is used for all species, both the lower and
upper bounds can be specified as single values. For the inverse-Gamma
prior on the spatial variances, here we set the shape parameter to 2 and
the scale parameter also equal to 2. For a more formal analysis, we may
want to do some exploratory data analysis to obtain a better guess for
the spatial variance for each species, and then replace the scale
parameter with this estimated guess for each species. For the spatial
decay parameter, we determine the bounds of the uniform distribution by
computing the smallest distance between sites and the largest distance
between sites. We then set the lower bound of the uniform to
3/max and the upper bound to 3/min, where
min and max correspond to the predetermined
distances between sites. Again, these are the default hyperparameter
values for the prior distribution of phi that
spOccupancy will assign.
# Minimum value is 0, so need to grab second element.
min.dist <- sort(unique(dist.hbef))[2]
max.dist <- max(dist.hbef)
ms.priors <- list(beta.comm.normal = list(mean = 0, var = 2.72),
alpha.comm.normal = list(mean = 0, var = 2.72),
tau.sq.beta.ig = list(a = 0.1, b = 0.1),
tau.sq.alpha.ig = list(a = 0.1, b = 0.1),
sigma.sq.ig = list(a = 2, b = 2),
phi.unif = list(a = 3 / max.dist, b = 3 / min.dist))We next set the parameters controlling the Adaptive MCMC algorithm
(see spPGOcc() section for details). Notice our
specification of the initial tuning values is exactly the same as for
spPGOcc. We assume the same initial tuning value for all
species. However, the adaptive algorithm will allow for species-specific
tuning parameters, so these will be adjusted in the algorithm as needed
(and reported to the R console if verbose = TRUE).
batch.length <- 25
n.batch <- 400
n.burn <- 2000
n.thin <- 20
n.chains <- 3
ms.tuning <- list(phi = 0.5)
n.omp.threads <- 1
# Values for reporting
verbose <- TRUE
n.report <- 100Spatially explicit multi-species occupancy models are currently the
most computationally intensive models fit by spOccupancy.
Even for modest sized data sets, we encourage the use of NNGPs instead
of full GPs when fitting spatially-explicit models to ease the
computational burden of fitting these models. We fit the model with an
NNGP below using 5 neighbors and summarize it using the
summary() function, where we specify that we want to
summarize both species and community-level parameters.
# Approx. run time: 10 min
out.sp.ms <- spMsPGOcc(occ.formula = occ.ms.sp.formula,
det.formula = det.ms.sp.formula,
data = hbef2015,
inits = ms.inits,
n.batch = n.batch,
batch.length = batch.length,
accept.rate = 0.43,
priors = ms.priors,
cov.model = cov.model,
tuning = ms.tuning,
n.omp.threads = n.omp.threads,
verbose = TRUE,
NNGP = TRUE,
n.neighbors = 5,
n.report = n.report,
n.burn = n.burn,
n.thin = n.thin,
n.chains = n.chains)----------------------------------------
Preparing to run the model
----------------------------------------
----------------------------------------
Building the neighbor list
----------------------------------------
----------------------------------------
Building the neighbors of neighbors list
----------------------------------------
----------------------------------------
Model description
----------------------------------------
NNGP Multi-species Occupancy Model with Polya-Gamma latent
variable fit with 373 sites and 12 species.
Samples per chain: 10000 (400 batches of length 25)
Burn-in: 2000
Thinning Rate: 20
Number of Chains: 3
Total Posterior Samples: 1200
Using the exponential spatial correlation model.
Using 5 nearest neighbors.
Source compiled with OpenMP support and model fit using 1 thread(s).
Adaptive Metropolis with target acceptance rate: 43.0
----------------------------------------
Chain 1
----------------------------------------
Sampling ...
Batch: 100 of 400, 25.00%
Species Parameter Acceptance Tuning
1 phi 16.0 0.60462
2 phi 12.0 0.65498
3 phi 32.0 0.48522
4 phi 68.0 0.60462
5 phi 84.0 0.40529
6 phi 24.0 0.37413
7 phi 28.0 0.39727
8 phi 28.0 0.64201
9 phi 44.0 0.31881
10 phi 68.0 0.45697
11 phi 44.0 0.33853
12 phi 52.0 0.39727
-------------------------------------------------
Batch: 200 of 400, 50.00%
Species Parameter Acceptance Tuning
1 phi 16.0 0.70953
2 phi 64.0 0.42183
3 phi 72.0 0.90199
4 phi 64.0 0.64201
5 phi 92.0 0.37413
6 phi 40.0 0.34537
7 phi 84.0 0.45697
8 phi 32.0 0.59265
9 phi 52.0 0.29430
10 phi 76.0 1.05850
11 phi 32.0 0.31250
12 phi 40.0 0.44792
-------------------------------------------------
Batch: 300 of 400, 75.00%
Species Parameter Acceptance Tuning
1 phi 36.0 0.69548
2 phi 24.0 0.65498
3 phi 12.0 1.19346
4 phi 76.0 0.54709
5 phi 32.0 0.39727
6 phi 52.0 0.30025
7 phi 68.0 0.53625
8 phi 36.0 0.60462
9 phi 40.0 0.31881
10 phi 48.0 1.51718
11 phi 44.0 0.28847
12 phi 20.0 0.43905
-------------------------------------------------
Batch: 400 of 400, 100.00%
----------------------------------------
Chain 2
----------------------------------------
Sampling ...
Batch: 100 of 400, 25.00%
Species Parameter Acceptance Tuning
1 phi 68.0 0.54709
2 phi 60.0 0.75341
3 phi 28.0 1.01700
4 phi 16.0 0.58092
5 phi 64.0 0.39727
6 phi 80.0 0.46620
7 phi 48.0 0.56941
8 phi 28.0 0.88413
9 phi 20.0 0.30025
10 phi 48.0 1.45769
11 phi 36.0 0.30025
12 phi 64.0 0.51523
-------------------------------------------------
Batch: 200 of 400, 50.00%
Species Parameter Acceptance Tuning
1 phi 16.0 0.60462
2 phi 76.0 1.19346
3 phi 32.0 1.07988
4 phi 32.0 0.50503
5 phi 84.0 0.42183
6 phi 36.0 0.51523
7 phi 32.0 0.65498
8 phi 52.0 0.60462
9 phi 48.0 0.29430
10 phi 32.0 1.21756
11 phi 48.0 0.32525
12 phi 28.0 0.39727
-------------------------------------------------
Batch: 300 of 400, 75.00%
Species Parameter Acceptance Tuning
1 phi 52.0 0.51523
2 phi 16.0 1.29285
3 phi 68.0 0.76863
4 phi 12.0 0.65498
5 phi 28.0 0.33853
6 phi 40.0 0.35234
7 phi 48.0 0.78416
8 phi 40.0 0.99686
9 phi 24.0 0.31881
10 phi 24.0 1.14666
11 phi 52.0 0.29430
12 phi 24.0 0.35946
-------------------------------------------------
Batch: 400 of 400, 100.00%
----------------------------------------
Chain 3
----------------------------------------
Sampling ...
Batch: 100 of 400, 25.00%
Species Parameter Acceptance Tuning
1 phi 28.0 0.47561
2 phi 8.0 1.05850
3 phi 24.0 0.93881
4 phi 40.0 0.54709
5 phi 28.0 0.43905
6 phi 28.0 0.35234
7 phi 24.0 0.56941
8 phi 56.0 0.64201
9 phi 32.0 0.29430
10 phi 80.0 1.34562
11 phi 32.0 0.31250
12 phi 40.0 0.43905
-------------------------------------------------
Batch: 200 of 400, 50.00%
Species Parameter Acceptance Tuning
1 phi 48.0 0.75341
2 phi 48.0 1.24216
3 phi 32.0 1.03754
4 phi 0.0 0.84947
5 phi 20.0 0.52564
6 phi 52.0 0.39727
7 phi 52.0 0.62930
8 phi 44.0 0.50503
9 phi 52.0 0.28847
10 phi 32.0 1.07988
11 phi 20.0 0.31250
12 phi 48.0 0.38169
-------------------------------------------------
Batch: 300 of 400, 75.00%
Species Parameter Acceptance Tuning
1 phi 12.0 0.95777
2 phi 12.0 1.03754
3 phi 72.0 1.26725
4 phi 80.0 0.95777
5 phi 60.0 0.37413
6 phi 24.0 0.59265
7 phi 12.0 0.66821
8 phi 32.0 0.47561
9 phi 40.0 0.30631
10 phi 52.0 1.21756
11 phi 32.0 0.27716
12 phi 56.0 0.41348
-------------------------------------------------
Batch: 400 of 400, 100.00%
summary(out.sp.ms, level = 'both')
Call:
spMsPGOcc(occ.formula = occ.ms.sp.formula, det.formula = det.ms.sp.formula,
data = hbef2015, inits = ms.inits, priors = ms.priors, tuning = ms.tuning,
cov.model = cov.model, NNGP = TRUE, n.neighbors = 5, n.batch = n.batch,
batch.length = batch.length, accept.rate = 0.43, n.omp.threads = n.omp.threads,
verbose = TRUE, n.report = n.report, n.burn = n.burn, n.thin = n.thin,
n.chains = n.chains)
Samples per Chain: 10000
Burn-in: 2000
Thinning Rate: 20
Number of Chains: 3
Total Posterior Samples: 1200
Run Time (min): 5.9592
----------------------------------------
Community Level
----------------------------------------
Occurrence Means (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) 0.3473 1.0102 -1.5734 0.3142 2.3612 1.0094 662
scale(Elevation) 0.3182 0.7218 -1.1548 0.3330 1.7355 1.0109 708
I(scale(Elevation)^2) -0.2419 0.3620 -0.9397 -0.2511 0.4466 1.0167 580
Occurrence Variances (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) 21.0684 11.8608 7.9046 17.9266 52.4907 1.0005 272
scale(Elevation) 6.6667 4.2571 1.9950 5.6049 19.0005 1.1441 141
I(scale(Elevation)^2) 1.2584 0.9880 0.2837 0.9798 4.0144 1.0168 213
Detection Means (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) -0.7479 0.4856 -1.7491 -0.7301 0.1782 1.0420 1075
scale(day) 0.0553 0.0819 -0.1064 0.0558 0.2212 1.0010 1200
scale(tod) -0.0423 0.0806 -0.2011 -0.0400 0.1106 1.0034 1200
I(scale(day)^2) -0.0243 0.0871 -0.1873 -0.0279 0.1606 1.0176 1200
Detection Variances (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) 2.6959 1.6985 0.8747 2.2608 6.8929 1.2435 71
scale(day) 0.0687 0.0396 0.0238 0.0585 0.1769 1.0000 1200
scale(tod) 0.0492 0.0297 0.0172 0.0419 0.1292 1.0163 1200
I(scale(day)^2) 0.0584 0.0394 0.0189 0.0477 0.1562 1.0078 1200
----------------------------------------
Species Level
----------------------------------------
Occurrence (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept)-AMRE -2.2815 2.7086 -6.4858 -2.9355 4.2689 1.9744 19
(Intercept)-BAWW 2.5365 2.0946 -0.7584 2.2198 7.0960 1.4755 32
(Intercept)-BHVI 4.0333 3.6977 -0.5973 2.9606 12.9948 1.0200 35
(Intercept)-BLBW 3.3087 0.9436 1.9473 3.1431 5.6469 1.0254 150
(Intercept)-BLPW -5.8360 1.0175 -8.3386 -5.7107 -4.1643 1.2592 140
(Intercept)-BTBW 4.8120 0.9071 3.4191 4.7038 6.9931 1.0448 162
(Intercept)-BTNW 3.4304 0.9695 2.1977 3.2224 6.0079 1.3040 50
(Intercept)-CAWA -3.1298 1.0008 -5.3939 -3.0320 -1.4304 1.0029 128
(Intercept)-MAWA -3.9025 1.3254 -6.8776 -3.7596 -1.6953 1.0289 109
(Intercept)-NAWA -3.1859 0.8399 -5.1576 -3.1373 -1.5230 1.0428 152
(Intercept)-OVEN 3.9623 1.1327 2.1991 3.7998 6.4261 1.1254 129
(Intercept)-REVI 4.4086 0.9473 3.0077 4.2737 6.7094 1.0219 108
scale(Elevation)-AMRE 1.4412 1.6675 -1.2066 1.2105 5.4484 1.1773 79
scale(Elevation)-BAWW -1.1371 1.2987 -4.9241 -0.7893 0.4232 1.4511 54
scale(Elevation)-BHVI 0.1555 1.3972 -2.9896 0.2408 2.7950 1.0513 291
scale(Elevation)-BLBW -0.5257 0.3356 -1.3335 -0.4889 0.0079 1.0075 413
scale(Elevation)-BLPW 3.2010 0.8262 1.9354 3.0894 5.0173 1.0179 378
scale(Elevation)-BTBW -0.6187 0.2852 -1.2238 -0.5994 -0.0766 1.0201 720
scale(Elevation)-BTNW 0.8550 0.4134 0.2184 0.7929 1.8104 1.0357 295
scale(Elevation)-CAWA 2.4929 0.9276 1.0612 2.3658 4.6667 1.0244 258
scale(Elevation)-MAWA 3.2930 1.0842 1.6200 3.1378 5.9472 1.2140 96
scale(Elevation)-NAWA 1.3789 0.5007 0.5983 1.3217 2.5665 1.0078 439
scale(Elevation)-OVEN -3.2116 0.8969 -5.2692 -3.1166 -1.7895 1.0665 121
scale(Elevation)-REVI -2.9916 1.0358 -5.3315 -2.8432 -1.4454 1.0411 178
I(scale(Elevation)^2)-AMRE -0.8601 0.9505 -2.8111 -0.8460 1.1943 1.1094 176
I(scale(Elevation)^2)-BAWW -1.3255 0.6778 -2.6943 -1.3252 0.0298 1.0446 141
I(scale(Elevation)^2)-BHVI 0.7021 1.0440 -1.0331 0.5814 3.3463 1.0260 128
I(scale(Elevation)^2)-BLBW -0.7186 0.2732 -1.3345 -0.6971 -0.2539 1.0057 288
I(scale(Elevation)^2)-BLPW 1.0249 0.5185 -0.0986 1.0645 1.9453 1.0343 226
I(scale(Elevation)^2)-BTBW -1.3915 0.3025 -2.0875 -1.3532 -0.8953 1.0313 213
I(scale(Elevation)^2)-BTNW -0.2161 0.2512 -0.7162 -0.2088 0.2710 1.0253 793
I(scale(Elevation)^2)-CAWA -0.7112 0.5865 -1.9519 -0.6604 0.2941 1.0294 377
I(scale(Elevation)^2)-MAWA 0.7289 0.5628 -0.3400 0.7064 1.9715 1.0190 386
I(scale(Elevation)^2)-NAWA 0.4062 0.3440 -0.2556 0.3896 1.0905 1.0034 650
I(scale(Elevation)^2)-OVEN -0.8508 0.4783 -1.8087 -0.8388 0.0398 1.0521 437
I(scale(Elevation)^2)-REVI 0.0360 0.5338 -0.9238 0.0087 1.1159 1.0242 339
Detection (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept)-AMRE -2.9091 1.4881 -5.5869 -2.6554 -0.4023 1.4879 27
(Intercept)-BAWW -2.6650 0.4069 -3.3606 -2.7135 -1.7885 1.4640 73
(Intercept)-BHVI -2.6829 0.2772 -3.1303 -2.7107 -2.0273 1.0466 62
(Intercept)-BLBW -0.0326 0.1337 -0.2922 -0.0284 0.2233 1.0056 802
(Intercept)-BLPW -0.4267 0.2613 -0.9853 -0.4251 0.0613 1.0071 1056
(Intercept)-BTBW 0.6347 0.1093 0.4177 0.6327 0.8414 1.0107 972
(Intercept)-BTNW 0.6018 0.1118 0.3824 0.6008 0.8201 1.0016 862
(Intercept)-CAWA -1.4642 0.5219 -2.5480 -1.4308 -0.4996 1.0103 421
(Intercept)-MAWA -0.7034 0.2208 -1.1430 -0.7065 -0.2413 1.0103 956
(Intercept)-NAWA -1.4819 0.5066 -2.5483 -1.4707 -0.5356 0.9993 347
(Intercept)-OVEN 0.8165 0.1213 0.5822 0.8140 1.0616 1.0007 1614
(Intercept)-REVI 0.5474 0.1114 0.3270 0.5495 0.7590 1.0013 1200
scale(day)-AMRE 0.0470 0.2389 -0.4224 0.0458 0.4861 1.0061 1200
scale(day)-BAWW 0.2143 0.1393 -0.0546 0.2106 0.4934 0.9993 1200
scale(day)-BHVI 0.2048 0.1237 -0.0363 0.2042 0.4596 1.0113 1200
scale(day)-BLBW -0.2252 0.0682 -0.3643 -0.2243 -0.0910 1.0091 1200
scale(day)-BLPW 0.0619 0.1648 -0.2499 0.0616 0.3731 1.0008 854
scale(day)-BTBW 0.2702 0.0682 0.1311 0.2768 0.3980 1.0079 1200
scale(day)-BTNW 0.1519 0.0678 0.0165 0.1536 0.2854 1.0139 1200
scale(day)-CAWA -0.0270 0.1771 -0.3818 -0.0281 0.2936 1.0033 1200
scale(day)-MAWA 0.1096 0.1257 -0.1360 0.1111 0.3425 1.0082 1298
scale(day)-NAWA 0.0204 0.1811 -0.3162 0.0199 0.3701 1.0017 1113
scale(day)-OVEN -0.0789 0.0748 -0.2197 -0.0800 0.0695 0.9999 1200
scale(day)-REVI -0.0722 0.0678 -0.2079 -0.0730 0.0592 0.9990 1200
scale(tod)-AMRE -0.0415 0.2169 -0.4466 -0.0386 0.3931 1.0211 1200
scale(tod)-BAWW -0.1789 0.1313 -0.4466 -0.1783 0.0558 1.0027 1340
scale(tod)-BHVI -0.0478 0.1107 -0.2590 -0.0470 0.1690 1.0097 1200
scale(tod)-BLBW 0.0596 0.0639 -0.0618 0.0611 0.1855 0.9989 1525
scale(tod)-BLPW 0.1047 0.1414 -0.1694 0.0972 0.3805 1.0065 1200
scale(tod)-BTBW -0.0338 0.0667 -0.1675 -0.0332 0.0919 1.0007 1200
scale(tod)-BTNW 0.0430 0.0635 -0.0844 0.0435 0.1663 1.0080 1005
scale(tod)-CAWA -0.2116 0.1742 -0.5894 -0.2077 0.1066 1.0164 1439
scale(tod)-MAWA 0.0213 0.1145 -0.2063 0.0229 0.2427 1.0015 1200
scale(tod)-NAWA -0.0679 0.1622 -0.3925 -0.0741 0.2549 1.0052 1371
scale(tod)-OVEN -0.0473 0.0731 -0.1853 -0.0500 0.0980 1.0088 1200
scale(tod)-REVI -0.0826 0.0671 -0.2083 -0.0827 0.0511 1.0057 1689
I(scale(day)^2)-AMRE -0.1188 0.2330 -0.6031 -0.1150 0.3301 1.0021 1088
I(scale(day)^2)-BAWW -0.0328 0.1482 -0.3142 -0.0314 0.2600 1.0035 1441
I(scale(day)^2)-BHVI 0.0571 0.1306 -0.2012 0.0608 0.3066 1.0159 1200
I(scale(day)^2)-BLBW -0.1726 0.0780 -0.3303 -0.1723 -0.0143 1.0007 1200
I(scale(day)^2)-BLPW 0.2049 0.1872 -0.1329 0.2009 0.6017 1.0024 1200
I(scale(day)^2)-BTBW -0.0635 0.0777 -0.2205 -0.0626 0.0925 1.0257 1200
I(scale(day)^2)-BTNW -0.0680 0.0767 -0.2168 -0.0707 0.0888 1.0065 1200
I(scale(day)^2)-CAWA -0.0388 0.1862 -0.3849 -0.0394 0.3440 1.0006 1200
I(scale(day)^2)-MAWA 0.0064 0.1377 -0.2674 0.0035 0.2865 1.0048 1200
I(scale(day)^2)-NAWA -0.1436 0.1833 -0.5131 -0.1378 0.2060 1.0068 1200
I(scale(day)^2)-OVEN 0.0155 0.0891 -0.1518 0.0147 0.1879 1.0025 1200
I(scale(day)^2)-REVI 0.0340 0.0804 -0.1210 0.0355 0.1912 1.0010 1200
Spatial Covariance:
Mean SD 2.5% 50% 97.5% Rhat ESS
sigma.sq-AMRE 2.4965 3.4245 0.4234 1.4272 13.4417 2.6708 51
sigma.sq-BAWW 2.4928 3.4658 0.3613 1.3010 13.6950 3.3678 12
sigma.sq-BHVI 2.2359 3.0873 0.3548 1.3103 10.6762 1.4210 62
sigma.sq-BLBW 2.6153 3.1885 0.3867 1.5961 11.4345 1.1973 58
sigma.sq-BLPW 2.2455 2.2236 0.3978 1.5702 8.6028 1.3926 31
sigma.sq-BTBW 2.3404 1.8247 0.4696 1.8221 7.3579 1.0977 97
sigma.sq-BTNW 3.6560 4.4047 0.4588 2.3306 16.9198 1.7161 53
sigma.sq-CAWA 3.0580 3.4678 0.4324 1.8098 13.2540 1.0055 62
sigma.sq-MAWA 13.3908 9.2710 2.5678 11.5642 36.9820 1.3652 79
sigma.sq-NAWA 1.8353 1.9814 0.3541 1.1860 7.3784 1.1416 91
sigma.sq-OVEN 9.8113 6.2705 2.4479 8.2358 26.6447 1.0975 137
sigma.sq-REVI 2.9019 2.4769 0.4802 2.2308 9.8657 1.0263 95
phi-AMRE 0.0123 0.0088 0.0009 0.0108 0.0292 1.2931 53
phi-BAWW 0.0143 0.0088 0.0007 0.0138 0.0293 1.4941 45
phi-BHVI 0.0150 0.0084 0.0014 0.0146 0.0291 1.1276 68
phi-BLBW 0.0126 0.0079 0.0018 0.0107 0.0288 1.0264 169
phi-BLPW 0.0074 0.0074 0.0006 0.0044 0.0271 1.0530 65
phi-BTBW 0.0069 0.0065 0.0008 0.0042 0.0251 1.2423 43
phi-BTNW 0.0121 0.0079 0.0021 0.0101 0.0286 1.0219 128
phi-CAWA 0.0113 0.0088 0.0008 0.0087 0.0290 1.2524 50
phi-MAWA 0.0019 0.0009 0.0006 0.0018 0.0040 1.0470 169
phi-NAWA 0.0162 0.0083 0.0024 0.0163 0.0295 1.0740 57
phi-OVEN 0.0023 0.0008 0.0008 0.0022 0.0040 1.0224 153
phi-REVI 0.0076 0.0071 0.0009 0.0049 0.0279 1.0237 70The resulting object out.sp.ms is a list of class
spMsPGOcc consisting primarily of posterior samples of all
community and species-level parameters, as well as some additional
objects that are used for summaries, predictions, and model fit
evaluation. The Rhat values indicate convergence of most community and
species-level parameters, but some parameters for rare species have not
yet converged and the ESS of many species-level parameters are quite
small. This is a clear reminder that spatially-explicit models often
have slow mixing rates, and so you will often need to run these models
for a large number of samples in order to achieve convergence and
adequate ESS.
Posterior predictive checks
We perform posterior predictive checks to assess Goodness of Fit
using ppcOcc() just as we have previously seen.
# Takes a few seconds to run.
ppc.sp.ms.out <- ppcOcc(out.sp.ms, 'freeman-tukey', group = 2)Currently on species 1 out of 12Currently on species 2 out of 12Currently on species 3 out of 12Currently on species 4 out of 12Currently on species 5 out of 12Currently on species 6 out of 12Currently on species 7 out of 12Currently on species 8 out of 12Currently on species 9 out of 12Currently on species 10 out of 12Currently on species 11 out of 12Currently on species 12 out of 12
summary(ppc.sp.ms.out, level = 'both')
Call:
ppcOcc(object = out.sp.ms, fit.stat = "freeman-tukey", group = 2)
Samples per Chain: 10000
Burn-in: 2000
Thinning Rate: 20
Number of Chains: 3
Total Posterior Samples: 1200
----------------------------------------
Community Level
----------------------------------------
Bayesian p-value: 0.509
----------------------------------------
Species Level
----------------------------------------
AMRE Bayesian p-value: 0.7508
BAWW Bayesian p-value: 0.5233
BHVI Bayesian p-value: 0.5642
BLBW Bayesian p-value: 0.2825
BLPW Bayesian p-value: 0.3842
BTBW Bayesian p-value: 0.4917
BTNW Bayesian p-value: 0.475
CAWA Bayesian p-value: 0.5742
MAWA Bayesian p-value: 0.595
NAWA Bayesian p-value: 0.61
OVEN Bayesian p-value: 0.39
REVI Bayesian p-value: 0.4675
Fit statistic: freeman-tukey Model selection using WAIC
Below we compute the WAIC using waicOcc() and compare it
to the WAIC for the non-spatial multi-species occupancy model.
waicOcc(out.sp.ms) elpd pD WAIC
-4203.321 307.357 9021.356
waicOcc(out.ms) elpd pD WAIC
-4531.90069 65.73988 9195.28116 As always, remember there is MC error in these numbers, and so the values you receive will be slightly different. The WAIC for the spatial model is considerably smaller than that for the nonspatial model, indicating the species-specific spatial processes improve prediction across the entire community. However, in a complete analysis we should ensure the models fully converge (and we have adequate ESS) before performing any model selection or comparison.
We can also compare the WAIC values individually for each species
using the by.sp argument.
waicOcc(out.sp.ms, by.sp = TRUE) elpd pD WAIC
1 -21.92025 5.07635 53.99319
2 -169.96464 10.63529 361.19986
3 -243.16825 7.27763 500.89176
4 -675.43470 35.06532 1421.00004
5 -123.90882 16.16024 280.13812
6 -672.22907 28.67682 1401.81178
7 -688.44906 46.69923 1470.29658
8 -91.02739 19.01812 220.09103
9 -200.44911 34.99128 470.88077
10 -94.68014 17.04331 223.44690
11 -555.89421 55.28479 1222.35799
12 -666.19523 31.42857 1395.24760
waicOcc(out.ms, by.sp = TRUE) elpd pD WAIC
1 -25.99821 2.077357 56.15113
2 -176.76426 5.644309 364.81713
3 -247.35736 3.961816 502.63835
4 -705.05523 7.323082 1424.75662
5 -139.52763 5.192069 289.43940
6 -699.31982 6.878930 1412.39750
7 -730.72192 6.556928 1474.55769
8 -107.98079 4.840212 225.64201
9 -261.84192 5.430174 534.54419
10 -106.69834 5.687815 224.77232
11 -632.92884 5.813987 1277.48565
12 -697.70637 6.333204 1408.07916k-fold cross-validation proceeds using the k.fold
argument as we have seen previously, returning a separate scoring rule
(deviance) for each species.
Prediction
Prediction with spMsPGOcc objects again uses the
predict() function given a set of covariates and spatial
coordinates of a set of locations. Results are very similar to the
nonspatial multi-species model, so we do not execute the following code,
since prediction in spatial models takes some time and run time is
multiplied by the number of species here.
Single-species integrated occupancy models
Data integration is a model-based approach that leverages multiple data sources to provide inference and prediction on some latent process of interest (Miller et al. 2019). Data integration is particularly relevant in ecology as many data sources are often collected to better understand a single ecological phenomenon, with each data source having advantages and disadvantages, say in terms of sample size, spatial extent, or data reliability. Often, multiple detection-nondetection data sources are available to study the occurrence and distribution of some species of interest. For example, both point count surveys performed by human observers and autonomous recording units could be used to monitor a bird species (Doser et al. 2021). Different types of data have different sources of observation error, which we should explicitly incorporate into a model to avoid attributing any variation in detection probability to the true ecological process. Here we describe single-species integrated occupancy models, which combine multiple sources of detection-nondetection data in a single hierarchical modeling framework. These data sources may or may not be replicated, but we note that the combination of two or more sources always results in a replicated data set.
Basic model description
The integrated occupancy model has an identical process model to that of the single-species occupancy model, but has a distinct detection model for each data source, each of which is conditional on the same, shared ecological process (i.e., species occurrence).
Let \(z_j\) be the presence or absence of a species at site \(j\), with \(j = 1, \dots, J\). We assume this latent occurrence variable arises from a Bernoulli process following
\[\begin{equation} \begin{split} &z_j \sim \text{Bernoulli}(\psi_j), \\ &\text{logit}(\psi_j) = \boldsymbol{x}^{\top}_j\boldsymbol{\beta}, \end{split} \end{equation}\]
where \(\psi_j\) is the probability of occurrence at site \(j\), which is a function of site-specific covariates \(\boldsymbol{X}\) and a vector of regression coefficients (\(\boldsymbol{\beta}\)).
We do not directly observe \(z_j\), but rather we observe an imperfect representation of the latent occurrence process. In integrated models, we have \(r = 1, \dots, R\) distinct sources of data that are all imperfect representations of a single, shared occurrence process. Let \(y_{r, a, k}\) be the observed detection (1) or nondetection (0) of a species of interest in data set \(r\) at site \(a\) during replicate \(k\). Because different data sources have different variables influencing the observation process, we envision a separate detection model for each data source that is defined conditional on a single, shared ecological process described above. We envision the detection-nondetection data from source \(r\) as arising from a Bernoulli process conditional on the true latent occurrence process:
\[\begin{equation} \begin{split} &y_{r, a, k} \sim \text{Bernoulli}(p_{r, a, k}z_{j[a]}), \\ &\text{logit}(p_{r, a, k}) = \boldsymbol{v}^{\top}_{r, a, k}\boldsymbol{\alpha}_r, \end{split} \end{equation}\]
where \(p_{r, a, k}\) is the probability of detecting a species at site \(a\) during replicate \(k\) (given it is present at site \(a\)) for data source \(r\), which is a function of site, replicate, and data source specific covariates \(\boldsymbol{V}_r\) and a vector of regression coefficients specific to each data source (\(\boldsymbol{\alpha}_r\)). Note that \(z_{j[a]}\) is the true occurrence status at site \(j\) corresponding to the \(a\)th data source site in the given data set \(r\). Each data source may be available at all \(J\) sites in the region of interest or at a subset of the \(J\) sites. Additionally, data sources can overlap in the sites they sample, or they can be obtained at distinct sites within all \(J\) sites of interest in the overall region.
We assume multivariate normal priors for the occurrence (\(\boldsymbol{\beta}\)) and data-set specific detection (\(\boldsymbol{\alpha}\)) regression coefficients to complete the Bayesian specification of a single-species occupancy model. Pólya-Gamma data augmentation is implemented in an analogous manner to that of the previous models to yield an efficient implementation of integrated occupancy models.
Example data sources: Ovenbird occurrence in the White Mountain National Forest
To illustrate an integrated occupancy model, we will use two data
sets that come from the White Mountain National Forest (WMNF) in New
Hampshire and Maine, USA. Our goal is to model the occurrence of OVEN in
the WMNF in 2015. Our first data source is the HBEF data set we have
used to illustrate all single data source models. Our second data source
comes from the National Ecological Observatory Network (NEON) at
Bartlett Experimental Forest (Barnett et al.
2019; National Ecological Observatory Network (NEON) 2021). The
Bartlett Forest and HBEF both lie within the larger WMNF. Suppose we are
interested in OVEN occurrence across the entire WMNF. By leveraging both
data sources in a single integrated model, we will expand the range of
covariates across which we can make reliable predictions, and may obtain
results that are more indicative across the entire region of interest
and not just a single data source location (Doser
et al. 2022). In this particular case, there is no overlap
between the two data sources (i.e., Bartlett Forest and HBEF do not
overlap spatially). However, the integrated occupancy models fit by
spOccupancy can integrate data sources with no overlap,
partial overlap, or complete overlap.
The NEON data are provided along with spOccupancy in the
neon2015 list. We load the NEON data along with the HBEF
data below
List of 4
$ y : num [1:12, 1:80, 1:3] 0 0 0 0 0 0 1 0 0 0 ...
$ occ.covs: num [1:80, 1] 390 425 443 382 441 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : NULL
.. ..$ : chr "Elevation"
$ det.covs:List of 2
..$ day: num [1:80] 169 169 169 169 169 169 169 169 169 170 ...
..$ tod: int [1:80] 8 8 6 7 8 6 7 7 7 8 ...
$ coords : num [1:80, 1:2] 318472 318722 318972 318472 318722 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:80] "1" "2" "3" "4" ...
.. ..$ : chr [1:2] "X" "Y"Details on the NEON data set are provided in the package
documentation as well as in Doser et al.
(2022). The NEON data are collected at 80 point count sites in
Bartlett Forest using a removal protocol with three time periods,
resulting in replicated detection-nondetection data that can be used in
an occupancy modeling framework (after reducing counts to binary
detection indicators). The neon2015 list, like the
hbef2015 object, contains the detection-nondetection data
for 12 foliage-gleaning bird species (y), occurrence
covariates stored in occ.covs, detection covariates stored
in det.covs, and the coordinates of the 80 point count
locations stored in coords. Below we subset the
detection-nondetection data in both data sources to solely work with
OVEN.
sp.names <- dimnames(hbef2015$y)[[1]]
ovenHBEF <- hbef2015
ovenHBEF$y <- ovenHBEF$y[sp.names == "OVEN", , ]
ovenNEON <- neon2015
ovenNEON$y <- ovenNEON$y[sp.names == "OVEN", , ]
table(ovenHBEF$y)
0 1
518 588
table(ovenNEON$y)
0 1
61 62 Thus, the ovenbird is observed in a little over half of the possible site/replicate combinations in both of the data sources.
Fitting single-species integrated occupancy models with
intPGOcc()
The function intPGOcc() fits single-species integrated
occupancy models in spOccupancy. Syntax is very similar to
that of single data source models, and specifically takes the following
form:
intPGOcc(occ.formula, det.formula, data, inits, n.samples, priors,
n.omp.threads = 1, verbose = TRUE, n.report = 1000,
n.burn = round(.10 * n.samples), n.thin = 1, n.chains = 1,
k.fold, k.fold.threads = 1, k.fold.seed, k.fold.data, k.fold.only = FALSE, ...)The data argument contains the list of data elements
necessary for fitting an integrated occupancy model. For nonspatial
integrated occupancy models, data should be a list
comprised of the following objects: y (list of
detection-nondetection data matrices for each data source),
occ.covs (data frame or matrix of covariates for occurrence
model), det.covs (a list of lists where each element of the
list corresponds to the detection-nondetection data for the given data
source), sites (a list where each element consists of the
site indices for the given data source.
The ovenHBEF and ovenNEON lists are
currently formatted for use in single data source models and so we need
to combine these data sources together. Perhaps the trickiest part of
data integration is ensuring each point count location in each data
source lines up with the correct geographical location where you want to
determine the true presence/absence of the species of interest. In
spOccupancy, most of this bookkeeping is done under the
hood, but we will need to combine the two data sources together into a
single list in which we are consistent about how the data sources are
sorted. To accomplish this, we recommend first creating the occurrence
covariates matrix for all data sources. Because our two data sources do
not overlap spatially, this is relatively simple here as we can just use
rbind().
num [1:453, 1] 475 494 546 587 588 ...
- attr(*, "dimnames")=List of 2
..$ : NULL
..$ : chr "Elevation"Notice the order in which we placed these covariates: all covariate
values for HBEF come first, followed by all covariates for NEON. We need
to ensure that we use this identical ordering for all objects in the
data list. Next, we create the site indices stored in
sites. sites should be a list with two
elements (one for each data source), where each element consists of a
vector that indicates the rows in occ.covs that correspond
with the specific row of the detection-nondetection data for that data
source. When the data sources stem from distinct points (like in our
current case), this is again relatively straightforward as the indices
simply correspond to how we ordered the points in
occ.covs.
sites.int <- list(hbef = 1:nrow(ovenHBEF$occ.covs),
neon = 1:nrow(ovenNEON$occ.covs) + nrow(ovenHBEF$occ.covs))
str(sites.int)List of 2
$ hbef: int [1:373] 1 2 3 4 5 6 7 8 9 10 ...
$ neon: int [1:80] 374 375 376 377 378 379 380 381 382 383 ...Next we create the combined detection-nondetection data
y. For integrated models in spOccupancy,
y is a list of matrices, with each element containing the
detection-nondetection matrix for the specific data source. Again, we
must ensure that we place the data sources in the correct order.
List of 2
$ hbef: num [1:373, 1:3] 1 1 0 1 0 0 1 0 1 1 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : chr [1:373] "1" "2" "3" "4" ...
.. ..$ : chr [1:3] "1" "2" "3"
$ neon: num [1:80, 1:3] 1 1 0 1 1 0 1 1 0 1 ...Lastly, we create the detection covariates det.covs.
This should be a list of the detection covariates from each individual
data source. Because individual data source detection covariates are
stored as lists for single data source models in
spOccupancy, det.covs is now a list of lists
for integrated occupancy models.
det.covs.int <- list(hbef = ovenHBEF$det.covs,
neon = ovenNEON$det.covs)Finally, we package everything together into a single list, which we
call data.int.
data.int <- list(y = y.int,
occ.covs = occ.covs.int,
det.covs = det.covs.int,
sites = sites.int)
str(data.int)List of 4
$ y :List of 2
..$ hbef: num [1:373, 1:3] 1 1 0 1 0 0 1 0 1 1 ...
.. ..- attr(*, "dimnames")=List of 2
.. .. ..$ : chr [1:373] "1" "2" "3" "4" ...
.. .. ..$ : chr [1:3] "1" "2" "3"
..$ neon: num [1:80, 1:3] 1 1 0 1 1 0 1 1 0 1 ...
$ occ.covs: num [1:453, 1] 475 494 546 587 588 ...
..- attr(*, "dimnames")=List of 2
.. ..$ : NULL
.. ..$ : chr "Elevation"
$ det.covs:List of 2
..$ hbef:List of 2
.. ..$ day: num [1:373, 1:3] 156 156 156 156 156 156 156 156 156 156 ...
.. ..$ tod: num [1:373, 1:3] 330 346 369 386 409 425 447 463 482 499 ...
..$ neon:List of 2
.. ..$ day: num [1:80] 169 169 169 169 169 169 169 169 169 170 ...
.. ..$ tod: int [1:80] 8 8 6 7 8 6 7 7 7 8 ...
$ sites :List of 2
..$ hbef: int [1:373] 1 2 3 4 5 6 7 8 9 10 ...
..$ neon: int [1:80] 374 375 376 377 378 379 380 381 382 383 ...We specify the occurrence and detection model formulas using the
occ.formula, and det.formula arguments. The
occ.formula remains unchanged from previous models, and we
will specify occurrence of the ovenbird as a function of linear and
quadratic terms of elevation.
For the detection models, we need to specify a different detection
model for each data source. We do this by supplying a list to the
det.formula argument, where each element of the list is the
model formula for that given data set. Here we specify the detection
model for HBEF as a function of linear and quadratic terms for ‘day of
survey’ as well as a linear term for ‘time of survey’. In this case, we
include the same covariates for the NEON model (though we note that
different coefficients are estimated for the two data sources). However,
there is no requirement for the data sources to be a function of the
same covariates.
det.formula.int = list(hbef = ~ scale(day) + scale(tod) + I(scale(day)^2),
neon = ~ scale(day) + scale(tod) + I(scale(day)^2))Next we specify the initial values. Initial values are specified in a
list with the following tags: z (latent occurrence values),
alpha (detection regression coefficients), and
beta (occurrence regression coefficients). This aligns with
fitting single-species occupancy models using PGOcc().
However, since we now have multiple detection models with different
coefficients for each data source, initial values for alpha
are now passed to intPGOcc() as a list, with each element
of the list corresponding to the initial detection parameter values for
a given data source. These are specified either as a vector with a value
for each parameter or a single value for all parameters).
# Total number of sites
J <- nrow(data.int$occ.covs)
inits.list <- list(alpha = list(0, 0),
beta = 0,
z = rep(1, J))We next specify the priors for all parameters in the integrated
occupancy model in a list that is passed into the priors
argument. We specify normal priors for both the occurrence and detection
regression coefficients, using tags beta.normal and
alpha.normal, respectively.
prior.list <- list(beta.normal = list(mean = 0, var = 2.72),
alpha.normal = list(mean = list(0, 0),
var = list(2.72, 2.72)))Priors for the occurrence regression coefficients are specified as we
have seen in previous models. Because we have multiple
detection-nondetection data sets each with distinct detection
parameters, we specify the hypermeans and hypervariances in individual
lists, where each element of the list corresponds to a specific data
source. Again, the ordering of the data sources in the lists must align
with the order the data sources are saved in the detection-nondetection
data supplied to the data argument.
Finally, we specify the number of samples, burn-in, and thinning rate using the same approach we have used for previous models.
n.samples <- 8000
n.burn <- 3000
n.thin <- 25We can now run the integrated occupancy model. Below we set the number of threads used to 1 and print out sampler progress after every 2000th iteration.
# Approx. run time: < 15 sec
out.int <- intPGOcc(occ.formula = occ.formula.int,
det.formula = det.formula.int,
data = data.int,
inits = inits.list,
n.samples = n.samples,
priors = prior.list,
n.omp.threads = 1,
verbose = TRUE,
n.report = 2000,
n.burn = n.burn,
n.thin = n.thin,
n.chains = 3) ----------------------------------------
Preparing to run the model
----------------------------------------
----------------------------------------
Model description
----------------------------------------
Integrated Occupancy Model with Polya-Gamma latent
variable fit with 453 sites.
Integrating 2 occupancy data sets.
Samples per Chain: 8000
Burn-in: 3000
Thinning Rate: 25
Number of Chains: 3
Total Posterior Samples: 600
Source compiled with OpenMP support and model fit using 1 thread(s).
----------------------------------------
Chain 1
----------------------------------------
Sampling ...
Sampled: 2000 of 8000, 25.00%
-------------------------------------------------
Sampled: 4000 of 8000, 50.00%
-------------------------------------------------
Sampled: 6000 of 8000, 75.00%
-------------------------------------------------
Sampled: 8000 of 8000, 100.00%
----------------------------------------
Chain 2
----------------------------------------
Sampling ...
Sampled: 2000 of 8000, 25.00%
-------------------------------------------------
Sampled: 4000 of 8000, 50.00%
-------------------------------------------------
Sampled: 6000 of 8000, 75.00%
-------------------------------------------------
Sampled: 8000 of 8000, 100.00%
----------------------------------------
Chain 3
----------------------------------------
Sampling ...
Sampled: 2000 of 8000, 25.00%
-------------------------------------------------
Sampled: 4000 of 8000, 50.00%
-------------------------------------------------
Sampled: 6000 of 8000, 75.00%
-------------------------------------------------
Sampled: 8000 of 8000, 100.00%We again make a call to the summary function for a
concise description of the model results.
summary(out.int)
Call:
intPGOcc(occ.formula = occ.formula.int, det.formula = det.formula.int,
data = data.int, inits = inits.list, priors = prior.list,
n.samples = n.samples, n.omp.threads = 1, verbose = TRUE,
n.report = 2000, n.burn = n.burn, n.thin = n.thin, n.chains = 3)
Samples per Chain: 8000
Burn-in: 3000
Thinning Rate: 25
Number of Chains: 3
Total Posterior Samples: 600
Run Time (min): 0.1083
----------------------------------------
Occurrence
----------------------------------------
Fixed Effects (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) 2.2624 0.2343 1.8219 2.2500 2.7436 0.9982 600
scale(Elevation) -1.2914 0.1950 -1.7649 -1.2760 -0.9742 1.0021 600
I(scale(Elevation)^2) -0.5914 0.1628 -0.8890 -0.5902 -0.2567 0.9999 600
----------------------------------------
Data source 1 Detection
----------------------------------------
Fixed Effects (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) 0.8092 0.1233 0.5563 0.8062 1.0519 1.0002 408
scale(day) -0.0931 0.0780 -0.2423 -0.0929 0.0643 1.0000 600
scale(tod) -0.0448 0.0800 -0.1979 -0.0458 0.1126 1.0084 600
I(scale(day)^2) 0.0270 0.0977 -0.1649 0.0274 0.2276 1.0003 461
----------------------------------------
Data source 2 Detection
----------------------------------------
Fixed Effects (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) 2.0627 0.5760 1.0045 2.0404 3.2290 1.0061 600
scale(day) 0.9241 0.3909 0.2559 0.8939 1.7901 1.0166 699
scale(tod) 0.8503 0.5339 -0.2729 0.9204 1.7673 1.0161 514
I(scale(day)^2) -0.7939 0.3342 -1.4319 -0.7822 -0.1278 1.0048 600The summary function for integrated models returns the
detection parameters separately for each detection covariate. The Rhat
and ESS values clearly indicate adequate convergence and mixing of the
MCMC chains. Looking at the occurrence parameters, we see fairly similar
estimates to those from the single data source model using HBEF data
only. Of course this is only a half-surprise due to the unequal sizes of
the two data sets, where the HBEF data will be expected to dominate
estimation of the occupancy parameters. But an alternative explanation
for the relative similarity is that the two processes are indeed very
similar in the two areas within the greater WMNF region.
Posterior predictive checks
We perform posterior predictive checks using ppcOcc() as
before. GoF assessment for integrated models is an active area of
research and no consensus has so far appeared on the best approach. In
spOccupancy, we compute posterior predictive checks
separately for each data set in the integrated model.
Call:
ppcOcc(object = out.int, fit.stat = "freeman-tukey", group = 2)
Samples per Chain: 8000
Burn-in: 3000
Thinning Rate: 25
Number of Chains: 3
Total Posterior Samples: 600
Data Source 1
Bayesian p-value: 0.3367
Fit statistic: freeman-tukey
Data Source 2
Bayesian p-value: 0.0983
Fit statistic: freeman-tukey The low Bayesian p-value for NEON suggests a potential lack of fit which we would explore in a complete analysis.
Model selection using WAIC and k-fold cross-validation
We use waicOcc() to compute the WAIC for integrated
occupancy models. Similar to the posterior predictive check, individual
WAIC values are reported for each data set. These can be summed across
all data sources for an overall WAIC value if desired.
waicOcc(out.int) elpd pD WAIC
1 -633.34387 5.898022 1278.4838
2 -57.87313 8.062032 131.8703k-fold cross-validation is implemented using the k.fold
argument as we have seen in previous spOccupancy model
fitting functions. Cross-validation for models with multiple data
sources is not as straightforward as single data source models. For
instance, we could envision splitting the data in multiple different
ways to assess predictive performance, depending on the purpose of our
comparison. In spOccupancy, we implement two approaches for
cross-validation of integrated occupancy models. In the first approach,
we hold out locations irrespective of what data source they came from.
This results in a scoring rule (deviance) for each individual data
source based on the hold out sites where that data source is sampled.
More specifically, our first algorithm for K-fold cross-validation
is:
- Randomly split the total number of sites with at least one data source into \(K\) groups.
- For each \(k = 1, \dots, K\), fit the model without the data at the sites in the \(k\)th group of hold-out locations.
- Predict the detection-nondetection data at the locations in the \(k\)th hold out set.
- Compute the deviance for each hold out data point.
- Sum the deviance values separately for each data source to yield a scoring rule for each data source separately.
This form of k-fold cross-validation is applicable for
model-selection between different integrated occupancy models. In other
words, this approach can be used to compare models that integrate the
same data sources but include different covariates in the occurrence
and/or detection portion of the occupancy model. Using our example, we
implement 4-fold cross-validation to compare the full integrated model
with covariates to an intercept only integrated occupancy model. We do
this using the k.fold, k.fold.threads, and
k.fold.seed arguments as with previous
spOccupancy models. Below we use the default values for
k.fold.threads and k.fold.seed.
out.int.k.fold <- intPGOcc(occ.formula = occ.formula.int,
det.formula = det.formula.int,
data = data.int,
inits = inits.list,
n.samples = n.samples,
priors = prior.list,
n.omp.threads = 1,
verbose = FALSE,
n.report = 2000,
n.burn = n.burn,
n.thin = n.thin,
n.chains = 1,
k.fold = 4)
out.int.k.fold.small <- intPGOcc(occ.formula = ~ 1,
det.formula = list(hbef = ~ 1, neon = ~ 1),
data = data.int,
inits = inits.list,
n.samples = n.samples,
priors = prior.list,
n.omp.threads = 1,
verbose = FALSE,
n.report = 2000,
n.burn = n.burn,
n.thin = n.thin,
n.chains = 1,
k.fold = 4)
# Summarize the CV results
out.int.k.fold$k.fold.deviance[1] 1333.4470 158.7553
out.int.k.fold.small$k.fold.deviance[1] 1531.4821 184.8508We see the deviance for the full model is lower for both data sources compared to the intercept only model.
Alternatively, we may not wish to compare different integrated
occupancy models together, but rather wish to assess whether or not data
integration is necessary compared to using a single data source
occupancy model. To accomplish this task, we can perform
cross-validation with the integrated occupancy model using only a single
data source as the hold out set, and then compare the deviance scoring
rule to a scoring rule obtained from cross-validation with a single data
source occupancy model. We accomplish this by using the argument
k.fold.data. If k.fold.data is specified as an
integer between 1 and the number of data sources integrated (in this
case 2), only the data source corresponding to that integer will be used
in the hold out and k-fold cross-validation process. If
k.fold.data is not specified, k-fold cross-validation holds
out data irrespective of the data sources at the given location. Here,
we set k.fold.data = 1 and compare the cross-validation
results of the integrated model to the occupancy model using only HBEF
we fit with PGOcc() (which is stored in the
out.k.fold object).
out.int.k.fold.hbef <- intPGOcc(occ.formula = occ.formula.int,
det.formula = det.formula.int,
data = data.int,
inits = inits.list,
n.samples = n.samples,
priors = prior.list,
n.omp.threads = 1,
verbose = TRUE,
n.report = 2000,
n.burn = n.burn,
n.thin = n.thin,
k.fold = 4,
k.fold.data = 1) ----------------------------------------
Preparing to run the model
----------------------------------------
----------------------------------------
Model description
----------------------------------------
Integrated Occupancy Model with Polya-Gamma latent
variable fit with 453 sites.
Integrating 2 occupancy data sets.
Samples per Chain: 8000
Burn-in: 3000
Thinning Rate: 25
Number of Chains: 1
Total Posterior Samples: 200
Source compiled with OpenMP support and model fit using 1 thread(s).
----------------------------------------
Chain 1
----------------------------------------
Sampling ...
Sampled: 2000 of 8000, 25.00%
-------------------------------------------------
Sampled: 4000 of 8000, 50.00%
-------------------------------------------------
Sampled: 6000 of 8000, 75.00%
-------------------------------------------------
Sampled: 8000 of 8000, 100.00%
----------------------------------------
Cross-validation
----------------------------------------Performing 4-fold cross-validation using 1 thread(s).Only holding out data from data source 1.
# Look at CV results again
# Single data source model
out.k.fold$k.fold.deviance[1] 1332.179
# Integrated model
out.int.k.fold.hbef$k.fold.deviance[1] 1333.824Here we see that integration of the two data sources does not improve predictive performance at HBEF alone. We should also do the same approach with the NEON data. We close this section by emphasizing that there are potentially numerous other benefits to data integration than just predictive performance that must be carefully considered when trying to determine if data integration is necessary or not. See Simmonds et al. (2020), the discussion in Doser et al. (2022), and Chapter 10 in AHM2 for more on this topic.
Prediction
Prediction for integrated occupancy models proceeds exactly as before
using predict(). Here we predict occurrence across HBEF for
comparison with the single data source models (and remember to load the
stars and ggplot2 packages).
# Make sure to standardize using mean and sd from fitted model
elev.pred <- (hbefElev$val - mean(data.int$occ.covs[, 1])) / sd(data.int$occ.covs[, 1])
X.0 <- cbind(1, elev.pred, elev.pred^2)
out.int.pred <- predict(out.int, X.0)
# Producing an SDM for HBEF alone (posterior mean)
plot.dat <- data.frame(x = hbefElev$Easting,
y = hbefElev$Northing,
mean.psi = apply(out.int.pred$psi.0.samples, 2, mean),
sd.psi = apply(out.int.pred$psi.0.samples, 2, sd))
dat.stars <- st_as_stars(plot.dat, dims = c('x', 'y'))
ggplot() +
geom_stars(data = dat.stars, aes(x = x, y = y, fill = mean.psi)) +
scale_fill_viridis_c(na.value = 'transparent') +
labs(x = 'Easting', y = 'Northing', fill = '',
title = 'Mean OVEN occurrence probability using intPGOcc') +
theme_bw()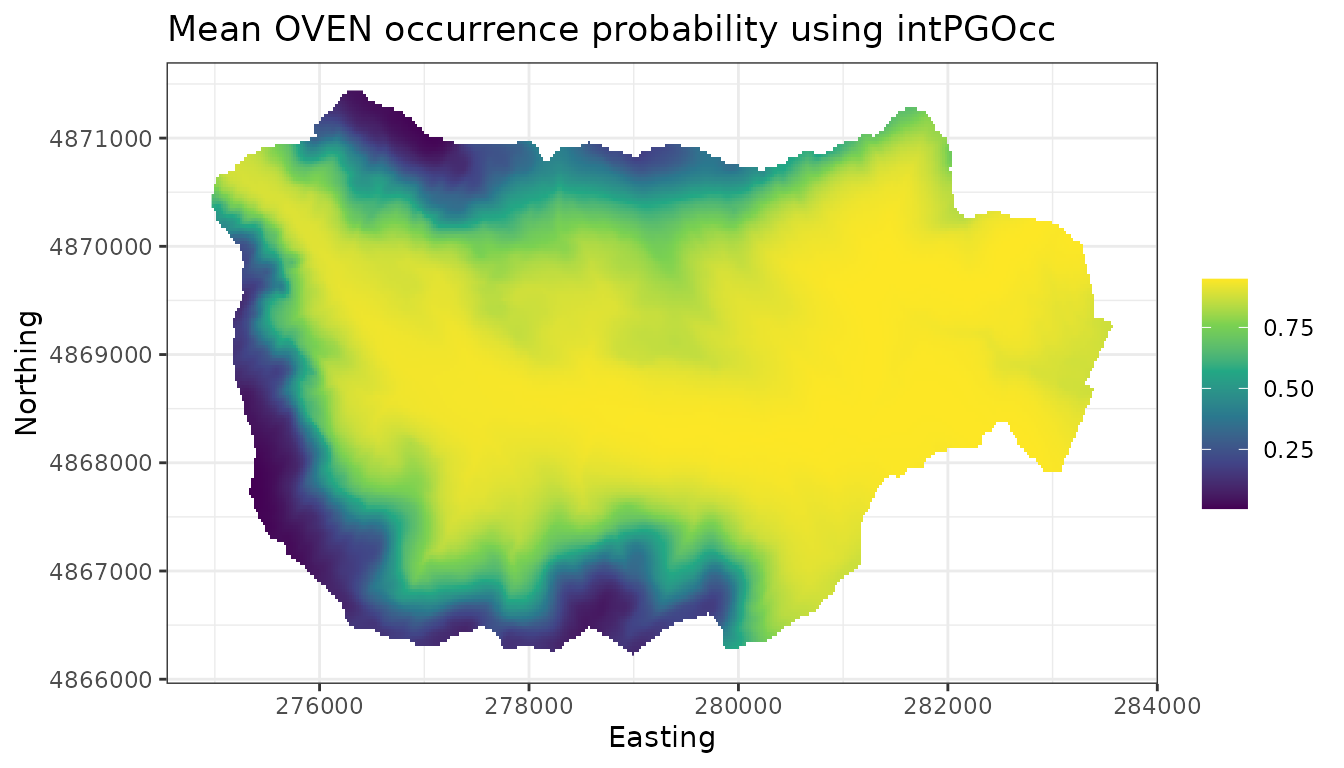
ggplot() +
geom_stars(data = dat.stars, aes(x = x, y = y, fill = sd.psi)) +
scale_fill_viridis_c(na.value = 'transparent') +
labs(x = 'Easting', y = 'Northing', fill = '',
title = 'SD OVEN occurrence probability using intPGOcc') +
theme_bw()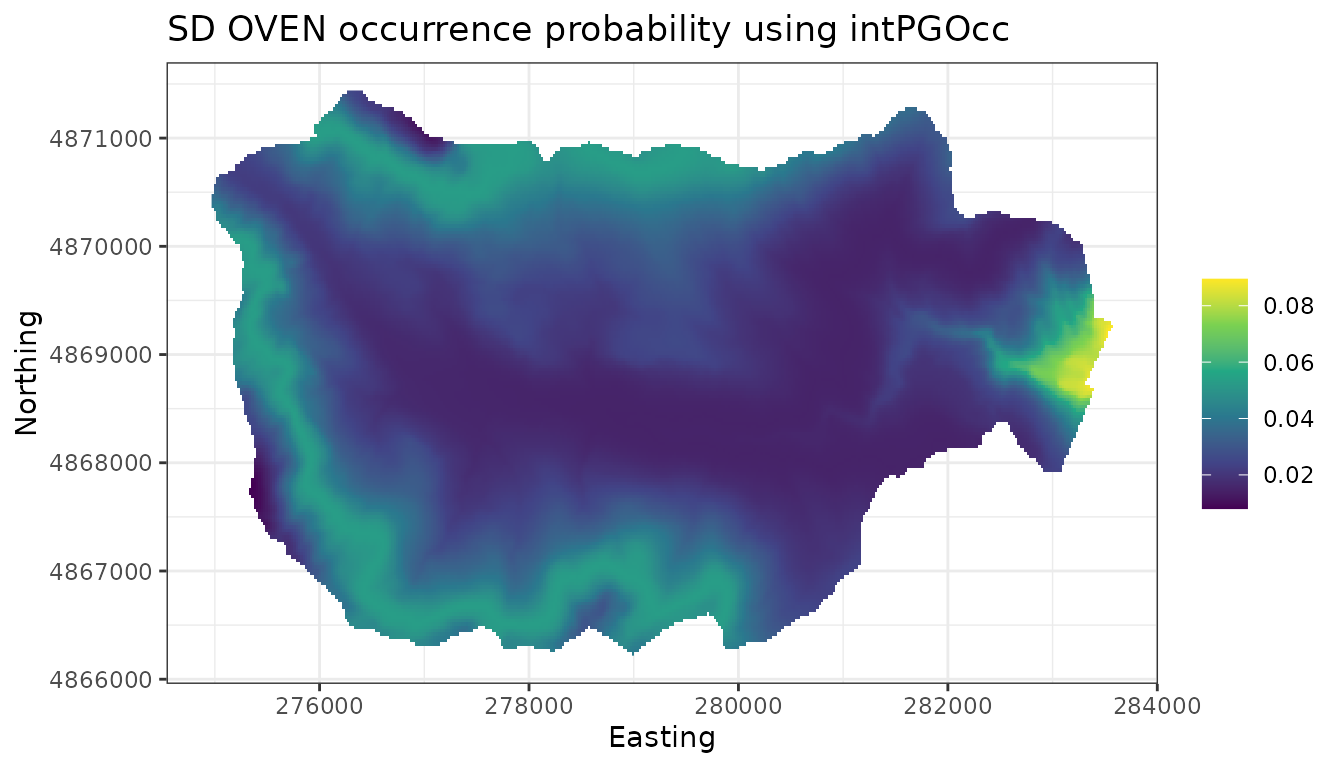
Single-species spatial integrated occupancy models
Basic model description
Single-species spatial integrated occupancy models are identical to integrated occupancy models except the ecological process model now incorporates a spatially-structured random effect following the discussion with single-species spatial occupancy models. All details for the single-species integrated spatial occupancy model have already been presented in previous model descriptions.
Fitting single-species spatial integrated occupancy models using
spIntPGOcc()
The function spIntPGOcc() fits single-species spatial
integrated occupancy models in spOccupancy. Syntax is very
similar to that of the single data source models and specifically takes
the following form:
spIntPGOcc(occ.formula, det.formula, data, inits, n.batch,
batch.length, accept.rate = 0.43, priors,
cov.model = "exponential", tuning, n.omp.threads = 1,
verbose = TRUE, NNGP = TRUE, n.neighbors = 15,
search.type = 'cb', n.report = 100,
n.burn = round(.10 * n.batch * batch.length),
n.thin = 1, n.chains = 1, k.fold, k.fold.threads = 1,
k.fold.seed, k.fold.data, k.fold.only = FALSE, ...)The occ.formula, det.formula, and
data arguments are analogous to what we saw with the
nonspatial integrated occupancy model. However, as for all spatial
models in spOccupancy, the data list must also
contain the spatial coordinates in the coords tag, which we
add below.
data.int$coords <- rbind(hbef2015$coords, neon2015$coords)
occ.formula.int <- ~ scale(Elevation) + I(scale(Elevation)^2)
det.formula.int <- list(hbef = ~ scale(day) + scale(tod) + I(scale(day)^2),
neon = ~ scale(day) + scale(tod) + I(scale(day)^2))Initial values specified in inits and priors in
priors are specified in the same form as for
intPGOcc() with the additional values for spatial
parameters. Analogous to all other spatial models in
spOccupancy, the spatial variance parameter takes an
inverse-Gamma prior and the spatial range parameter (as well as the
spatial smoothness parameter if cov.model = 'matern') takes
a uniform prior (see discussion in single-species spatial occupancy
models section on how to specify a uniform prior for the spatial
variance parameter instead of an inverse-Gamma).
dist.int <- dist(data.int$coords)
min.dist <- min(dist.int)
max.dist <- max(dist.int)
J <- nrow(data.int$occ.covs)
# Exponential covariance model
cov.model <- "exponential"
inits.list <- list(alpha = list(0, 0),
beta = 0,
z = rep(1, J),
sigma.sq = 2,
phi = 3 / mean(dist.int),
w = rep(0, J))
prior.list <- list(beta.normal = list(mean = 0, var = 2.72),
alpha.normal = list(mean = list(0, 0),
var = list(2.72, 2.72)),
sigma.sq.ig = c(2, 1),
phi.unif = c(3 / max.dist, 3 / min.dist))Finally, we specify the remaining parameters regarding the NNGP
specifications, tuning parameters, and the length of the MCMC sampler we
will run. We are then all set to fit the model. Remember that
spatially-explicit models in spOccupancy are implemented
using an efficient adaptive MCMC sampler that requires us to specify the
number of MCMC batches (n.batch) and the length of each
MCMC batch (batch.length), which together determine the
number of MCMC samples (i.e.,
n.samples = n.batch * batch.length). We run the model and
summarize the results with summary().
batch.length <- 25
n.batch <- 800
n.burn <- 10000
n.thin <- 40
tuning <- list(phi = .2)
# Approx. run time: 2 min
out.sp.int <- spIntPGOcc(occ.formula = occ.formula.int,
det.formula = det.formula.int,
data = data.int,
inits = inits.list,
priors = prior.list,
tuning = tuning,
cov.model = cov.model,
NNGP = TRUE,
n.neighbors = 5,
n.batch = n.batch,
n.burn = n.burn,
n.chains = 3,
batch.length = batch.length,
n.report = 200) ----------------------------------------
Preparing to run the model
----------------------------------------
----------------------------------------
Building the neighbor list
----------------------------------------
----------------------------------------
Building the neighbors of neighbors list
----------------------------------------
----------------------------------------
Model description
----------------------------------------
NNGP Spatial Integrated Occupancy Model with Polya-Gamma latent
variable fit with 453 sites.
Integrating 2 occupancy data sets.
Samples per chain: 20000 (800 batches of length 25)
Burn-in: 10000
Thinning Rate: 1
Number of Chains: 3
Total Posterior Samples: 30000
Using the exponential spatial correlation model.
Using 5 nearest neighbors.
Source compiled with OpenMP support and model fit using 1 thread(s).
Adaptive Metropolis with target acceptance rate: 43.0
----------------------------------------
Chain 1
----------------------------------------
Sampling ...
Batch: 200 of 800, 25.00%
Parameter Acceptance Tuning
phi 44.0 0.22326
-------------------------------------------------
Batch: 400 of 800, 50.00%
Parameter Acceptance Tuning
phi 44.0 0.22326
-------------------------------------------------
Batch: 600 of 800, 75.00%
Parameter Acceptance Tuning
phi 36.0 0.21025
-------------------------------------------------
Batch: 800 of 800, 100.00%
----------------------------------------
Chain 2
----------------------------------------
Sampling ...
Batch: 200 of 800, 25.00%
Parameter Acceptance Tuning
phi 44.0 0.22326
-------------------------------------------------
Batch: 400 of 800, 50.00%
Parameter Acceptance Tuning
phi 32.0 0.22777
-------------------------------------------------
Batch: 600 of 800, 75.00%
Parameter Acceptance Tuning
phi 36.0 0.21883
-------------------------------------------------
Batch: 800 of 800, 100.00%
----------------------------------------
Chain 3
----------------------------------------
Sampling ...
Batch: 200 of 800, 25.00%
Parameter Acceptance Tuning
phi 56.0 0.22777
-------------------------------------------------
Batch: 400 of 800, 50.00%
Parameter Acceptance Tuning
phi 44.0 0.21450
-------------------------------------------------
Batch: 600 of 800, 75.00%
Parameter Acceptance Tuning
phi 52.0 0.22777
-------------------------------------------------
Batch: 800 of 800, 100.00%
summary(out.sp.int)
Call:
spIntPGOcc(occ.formula = occ.formula.int, det.formula = det.formula.int,
data = data.int, inits = inits.list, priors = prior.list,
tuning = tuning, cov.model = cov.model, NNGP = TRUE, n.neighbors = 5,
n.batch = n.batch, batch.length = batch.length, n.report = 200,
n.burn = n.burn, n.chains = 3)
Samples per Chain: 20000
Burn-in: 10000
Thinning Rate: 1
Number of Chains: 3
Total Posterior Samples: 30000
Run Time (min): 1.2714
----------------------------------------
Occurrence
----------------------------------------
Fixed Effects (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) 2.8425 0.8146 0.8801 2.8965 4.3039 1.0472 201
scale(Elevation) -2.1704 0.5781 -3.4522 -2.1037 -1.2416 1.0312 258
I(scale(Elevation)^2) -0.9546 0.3613 -1.7384 -0.9303 -0.3082 1.0047 823
----------------------------------------
Data source 1 Detection
----------------------------------------
Fixed Effects (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) 0.8245 0.1237 0.5866 0.8230 1.0678 1.0006 19832
scale(day) -0.0930 0.0779 -0.2460 -0.0927 0.0587 1.0010 23358
scale(tod) -0.0464 0.0782 -0.2002 -0.0461 0.1050 1.0004 23097
I(scale(day)^2) 0.0287 0.0960 -0.1572 0.0285 0.2167 1.0012 21261
----------------------------------------
Data source 2 Detection
----------------------------------------
Fixed Effects (logit scale):
Mean SD 2.5% 50% 97.5% Rhat ESS
(Intercept) 2.1379 0.6081 0.9490 2.1339 3.3385 1.0021 2925
scale(day) 0.6673 0.5516 -0.5796 0.7202 1.6361 1.0061 1094
scale(tod) 0.4470 0.6128 -0.7485 0.4479 1.5806 1.0081 1653
I(scale(day)^2) -0.4500 0.6676 -1.4354 -0.6001 1.1273 1.0029 702
----------------------------------------
Spatial Covariance
----------------------------------------
Mean SD 2.5% 50% 97.5% Rhat ESS
sigma.sq 7.3723 5.3519 1.7459 6.0793 21.0828 1.1836 85
phi 0.0018 0.0008 0.0005 0.0017 0.0037 1.0200 142We see the occurrence and detection parameters have converged. We should run the chains for a bit longer to ensure convergence of the spatial covariance parameters, but for this example we will continue on.
Posterior predictive checks
Below we perform a posterior predictive check for each of the data
sets included in the occupancy model using ppcOcc().
Call:
ppcOcc(object = out.sp.int, fit.stat = "freeman-tukey", group = 2)
Samples per Chain: 20000
Burn-in: 10000
Thinning Rate: 1
Number of Chains: 3
Total Posterior Samples: 30000
Data Source 1
Bayesian p-value: 0.36
Fit statistic: freeman-tukey
Data Source 2
Bayesian p-value: 0.2413
Fit statistic: freeman-tukey According to the Bayesian p-values, there is no lack of fit for either the HBEF or NEON data.
Model selection using WAIC and k-fold cross-validation
We can perform model selection using WAIC with the
waicOcc() function as we have seen previously. Here we
compare the WAIC from the spatial integrated model to the non-spatial
integrated model.
waicOcc(out.int) elpd pD WAIC
1 -633.34387 5.898022 1278.4838
2 -57.87313 8.062032 131.8703
waicOcc(out.sp.int) elpd pD WAIC
1 -564.86896 49.04327 1227.8245
2 -43.39224 19.11941 125.0233We see the spatial model performs better for both the HBEF data and the NEON data.
Two forms of k-fold cross-validation are implemented for
spIntPGOcc(), analogous to those discussed for non-spatial
integrated occupancy models. We first use cross-validation to compare
the predictive performance of the spatial integrated model to the
nonspatial integrated model across all sites.
out.sp.int.k.fold <- spIntPGOcc(occ.formula = occ.formula.int,
det.formula = det.formula.int,
data = data.int,
inits = inits.list,
priors = prior.list,
tuning = tuning,
cov.model = cov.model,
NNGP = TRUE,
n.neighbors = 5,
n.batch = n.batch,
n.burn = n.burn,
batch.length = batch.length,
verbose = FALSE,
k.fold = 4)
# Non-spatial model
out.int.k.fold$k.fold.deviance[1] 1333.4470 158.7553
# Spatial model
out.sp.int.k.fold$k.fold.deviance[1] 1276.8537 169.2276Further, we perform cross-validation using only the HBEF data source as a hold out data source to compare with single data source models to assess the benefit of integration.
out.sp.int.k.fold.hbef <- spIntPGOcc(occ.formula = occ.formula.int,
det.formula = det.formula.int,
data = data.int,
inits = inits.list,
priors = prior.list,
tuning = tuning,
cov.model = cov.model,
NNGP = TRUE,
n.neighbors = 5,
n.batch = n.batch,
n.burn = n.burn,
batch.length = batch.length,
verbose = FALSE,
k.fold = 4,
k.fold.data = 1)
out.sp.int.k.fold.hbef$k.fold.deviance[1] 1276.953
# Non-spatial single data source model
out.k.fold$k.fold.deviance[1] 1332.179Prediction
Prediction for spatial integrated occupancy models proceeds exactly analogous to our approach using nonspatial integrated occupancy models. The only difference is that now we must also provide the coordinates of the nonsampled locations. The following code is not run as it provides similar results to the nonspatial integrated occupancy model.